Bài 29 trang 135 sách bài tập Toán 9 Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 29 trang 135 SBT Toán 9 Cánh Diều tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
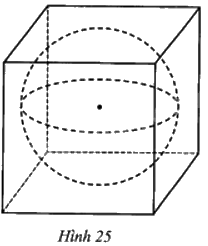
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?
Đề bài
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
Ta có lượng nước bị trào ra khỏi bể bằng thể tích hình cầu và bằng \(\frac{4}{3}\pi {a^3}\).
Thể tích của bể nước có dạng hình lập phương đó là: (2a)3 = 8a3.
Do đó, lượng nước còn lại trong bể là: \(8{a^3} - \frac{4}{3}\pi {a^3} = \frac{{\left( {24 - 4\pi } \right){a^3}}}{3}\).
Ta có tỉ số phần trăm của lượng nước còn lại trong bể và lượng nước bị trào ra khỏi bể là: \(\left[ {\frac{{\left( {24 - 4\pi } \right){a^3}}}{3}:\left( {\frac{4}{3}\pi {a^3}} \right)} \right].100\% \approx 91,1\% \).
Vậy lượng nước còn lại trong bể bằng khoảng 91,1% lượng nước bị trào ra khỏi bể.
Trước khi đi vào giải chi tiết bài 29 trang 135 SBT Toán 9 Cánh Diều tập 2, chúng ta cần ôn lại một số kiến thức cơ bản về hàm số bậc hai. Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0). Đồ thị của hàm số bậc hai là một parabol.
Để giải bài toán liên quan đến hàm số bậc hai, chúng ta cần nắm vững các phương pháp sau:
Đề bài: (SBT Toán 9 Cánh Diều tập 2, trang 135) Cho hàm số y = x2 - 4x + 3.
1. Tìm tọa độ đỉnh của parabol:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c với a = 1, b = -4, c = 3.
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh của parabol là y0 = x02 - 4x0 + 3 = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2; -1).
2. Tìm trục đối xứng của parabol:
Trục đối xứng của parabol là đường thẳng x = x0 = 2.
3. Xác định khoảng đồng biến, nghịch biến của hàm số:
Vì a = 1 > 0 nên hàm số đồng biến trên khoảng (2; +∞) và nghịch biến trên khoảng (-∞; 2).
4. Vẽ đồ thị của hàm số:
Để vẽ đồ thị của hàm số y = x2 - 4x + 3, ta thực hiện các bước sau:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 0 |
| 3 | 0 |
| 4 | 3 |
Vẽ parabol đi qua các điểm đã xác định và có đỉnh là (2; -1), trục đối xứng là x = 2.
Để củng cố kiến thức về hàm số bậc hai, các em có thể luyện tập thêm các bài tập sau:
Bài 29 trang 135 SBT Toán 9 Cánh Diều tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc hai và các phương pháp giải liên quan. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em sẽ tự tin hơn khi làm bài tập Toán 9.