Bài 3 trang 106 sách bài tập Toán 9 Cánh diều tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số, tìm đỉnh của parabol, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 106 sách bài tập Toán 9 Cánh diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy vẽ một số đa giác (lồi) mà các đỉnh là một số điểm trong các điểm đã cho ở Hình 7.
Đề bài
Hãy vẽ một số đa giác (lồi) mà các đỉnh là một số điểm trong các điểm đã cho ở Hình 7.
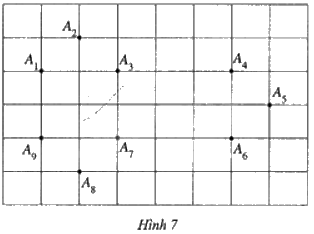
Phương pháp giải - Xem chi tiết
Dựa vào: Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó.
Lời giải chi tiết
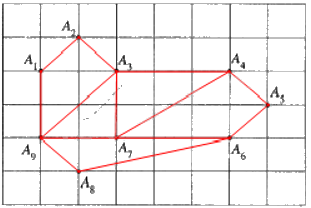
Ta có thể vẽ một số đa giác lồi như sau: tứ giác A1A2A3A9; tứ giác A3A4A7A9; tứ giác A4A5A6A7; ngũ giác A1A2A3A7A9; ngũ giác A3A4A5A6A7; ngũ giác A3A4A5A6A9; lục giác A3A4A5A6A8A9; …
Bài 3 trang 106 sách bài tập Toán 9 Cánh diều tập 2 thuộc chương trình học về hàm số bậc hai. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập. Giả sử bài tập yêu cầu:
“Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.”
| x | y |
|---|---|
| 0 | 3 |
| 1 | 0 |
| 2 | -1 |
| 3 | 0 |
| 4 | 3 |
Ngoài bài tập trên, còn rất nhiều dạng bài tập tương tự liên quan đến hàm số bậc hai. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc hai và luyện tập thường xuyên. Ngoài ra, việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị cũng có thể giúp học sinh giải bài tập nhanh chóng và chính xác hơn.
Học hàm số bậc hai có thể gặp nhiều khó khăn đối với học sinh. Dưới đây là một số lời khuyên giúp các em học tập hiệu quả hơn:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 3 trang 106 sách bài tập Toán 9 Cánh diều tập 2 và các bài tập tương tự. Chúc các em học tốt!