Bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Điểm kiểm tra môn Toán của 200 học sinh khối 9 được thống kê như Bảng 25 sau: a) Lập bảng tần số tương đối của mẫu số liệu thống kê đó. b) Vẽ biểu đồ tần số tương đối (ở đạng biểu đồ cột và biểu đồ hình quạt tròn) của mẫu số liệu thống kê đó.
Đề bài
Điểm kiểm tra môn Toán của 200 học sinh khối 9 được thống kê như Bảng 25 sau:

a) Lập bảng tần số tương đối của mẫu số liệu thống kê đó.
b) Vẽ biểu đồ tần số tương đối (ở đạng biểu đồ cột và biểu đồ hình quạt tròn) của mẫu số liệu thống kê đó.
Phương pháp giải - Xem chi tiết
a) Tính tỉ số % của mỗi đối tượng.
b) Xác định số đo cung tương ứng: x% tương ứng với x.3,6⁰.
Lời giải chi tiết
a) Tỉ số phần trăm của các giá trị \({x_1} = 5;{x_2} = 6;{x_3} = 7;{x_4} = 8;{x_5} = 9;{x_6} = 10\) lần lượt là:
\(\begin{array}{l}\frac{{30}}{{200}}.100\% = 15\% ,\frac{{40}}{{200}}.100\% = 20\% ,\frac{{50}}{{200}}.100\% = 25\% ,\frac{{35}}{{200}}.100\% = 17,5\%, \\\frac{{25}}{{200}}.100\% = 12,5\% ,\frac{{20}}{{200}}.100\% = 10\% \end{array}\)
Bảng tần số tương đối.

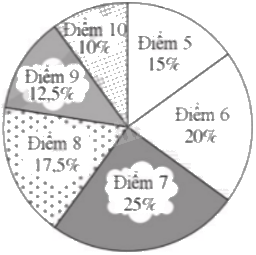
b) Số đo các góc trong biểu đồ quạt tròn của số điểm 5,6,7,8,9,10 lần lượt là:
\(15.3,6^\circ = 54^\circ ;20.3,6^\circ = 72^\circ ;25.3,6^\circ = 90^\circ ;\\17,5.3,6^\circ = 63^\circ ;12,5.3,6^\circ = 45^\circ ;10.3,6^\circ = 36^\circ. \)
Biểu đồ hình quạt tròn
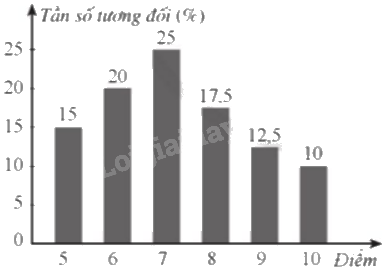
Biểu đồ cột
Bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2 thường bao gồm các dạng bài tập sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2:
Để xác định hệ số a của hàm số y = ax + b khi biết đồ thị của hàm số, ta có thể sử dụng phương pháp sau:
Ví dụ: Cho đồ thị của hàm số y = ax + b đi qua hai điểm A(1; 2) và B(2; 4). Ta có:
Giải hệ phương trình trên, ta được a = 2 và b = 0. Vậy hàm số cần tìm là y = 2x.
Để tìm tọa độ giao điểm của hai đường thẳng, ta có thể sử dụng phương pháp sau:
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.
Giải hệ phương trình:
Ta có: 2x + 1 = -x + 4 => 3x = 3 => x = 1. Thay x = 1 vào phương trình y = 2x + 1, ta được y = 3. Vậy tọa độ giao điểm của hai đường thẳng là (1; 3).
Các bài toán thực tế liên quan đến hàm số bậc nhất thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề trong cuộc sống. Ví dụ:
Một người đi xe máy với vận tốc 40km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Bài giải: Quãng đường đi được là: 40 * 2 = 80 km.
Bài 16 trang 21 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.