Bài 29 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 29 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh: a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp. b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Đề bài
Cho tam giác ABC nhọn. Ba đường cao AI, BK, CL. Chứng minh:
a) Các tứ giác AKIB, BLKC là các tứ giác nội tiếp.
b) Trực tâm H của tam giác ABC là tâm đường tròn nội tiếp tam giác IKL.
Phương pháp giải - Xem chi tiết
Dựa vào: Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc.
Chứng minh KH, LH là đường phân giác của góc LKI nên H tâm đường tròn nội tiếp tam giác IKL.
Lời giải chi tiết
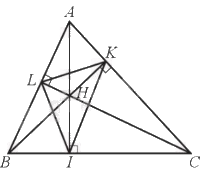
a) Ta có \(\widehat {AKB} = \widehat {AIB} = {90^o}\) (BK, AI là đường cao)
Nên tam giác AKB và AIB là tam giác vuông nên nội tiếp đường tròn đường kính AB. Do đó tứ giác AKIB là các tứ giác nội tiếp.
Ta có \(\widehat {BLC} = \widehat {BKC} = {90^o}\) (LC, BK là đường cao)
Nên tam giác BLC và BKC là tam giác vuông nên nội tiếp đường tròn đường kính BC. Do đó BLKC là các tứ giác nội tiếp.
b) Do tứ giác AKIB nội tiếp đường tròn nên \(\widehat {IKC} = \widehat {ABI}( = {180^o} - \widehat {AKI})\) hay \(\widehat {IKC} = \widehat {ABC}\). Tương tự \(\widehat {AKL} = \widehat {ABC}\). Suy ra \(\widehat {AKL} = \widehat {IKC}\).
Từ đó ta có \({90^o} - \widehat {AKL} = {90^o} - \widehat {IKC}\) hay \(\widehat {LKH} = \widehat {IKH}\). Vì vậy KH là đường phân giác của góc LKI. Tương tự cũng có LH là đường phân giác của góc KLI.
Vậy H tâm đường tròn nội tiếp tam giác IKL.
Bài 29 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương Hàm số bậc hai. Bài tập này thường xoay quanh việc xác định hệ số a, b, c của hàm số, tìm đỉnh của parabol, và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng câu hỏi cụ thể trong bài tập. Tuy nhiên, dưới đây là một ví dụ minh họa cách giải một dạng bài tập thường gặp trong bài 29:
Cho hàm số y = 2x2 - 4x + 1. Hãy tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.
| x | y |
|---|---|
| 0 | 1 |
| 1 | -1 |
| 2 | 1 |
Ngoài ví dụ minh họa trên, bài 29 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 còn có thể xuất hiện các dạng bài tập sau:
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, bạn nên:
Bài 29 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.