Bài 8 trang 82 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 82 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).
Đề bài
Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).
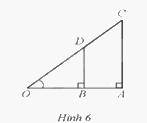
Phương pháp giải - Xem chi tiết
Bước 1: Chứng minh \(BD//CA\), sau đó áp dụng định lý Thales để suy ra \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\).
Bước 2: Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Bước 3: \(\cos \widehat {AOC} = \frac{{OA}}{{OC}}\), từ đó suy ra số đo góc AOC.
Lời giải chi tiết
Ta có: \(BD \bot OA,CA \bot OA\) nên \(BD//CA\).
Xét tam giác OAC có \(BD//CA\), áp dụng định lý Thales, ta được: \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\)
Suy ra \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Vì tam giác OAC vuông tại A nên ta có \(\cos \widehat {AOC} = \frac{{OA}}{{OC}} = \frac{3}{4}\), do đó \(\widehat {AOC} \approx 41^\circ \).
Bài 8 trong sách bài tập Toán 9 Cánh diều tập 1 tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất vào các bài toán thực tế. Cụ thể, bài tập yêu cầu học sinh xác định hệ số góc của đường thẳng, kiểm tra tính song song và vuông góc của các đường thẳng, và tìm phương trình đường thẳng thỏa mãn các điều kiện cho trước.
Bài 8 bao gồm các câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh khác nhau của hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm sau:
Câu a yêu cầu xác định hệ số góc của đường thẳng. Để làm được điều này, học sinh cần đưa phương trình đường thẳng về dạng y = ax + b, sau đó xác định giá trị của a.
Ví dụ: Nếu phương trình đường thẳng là 2x + 3y = 6, ta có thể viết lại thành y = (-2/3)x + 2. Vậy hệ số góc của đường thẳng là -2/3.
Câu b yêu cầu kiểm tra xem hai đường thẳng có song song hay không. Để làm được điều này, học sinh cần so sánh hệ số góc của hai đường thẳng. Nếu hai đường thẳng có cùng hệ số góc và khác tung độ gốc, chúng song song.
Ví dụ: Đường thẳng y = 2x + 1 và y = 2x - 3 có cùng hệ số góc là 2 và khác tung độ gốc, vậy chúng song song.
Câu c yêu cầu tìm phương trình đường thẳng thỏa mãn các điều kiện cho trước. Để làm được điều này, học sinh cần sử dụng các công thức về phương trình đường thẳng, kết hợp với các điều kiện đã cho để tìm ra các hệ số a và b.
Ví dụ: Tìm phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc là 3. Ta có thể sử dụng công thức y - y1 = m(x - x1), trong đó (x1; y1) là tọa độ của điểm A và m là hệ số góc. Thay số vào, ta được y - 2 = 3(x - 1), hay y = 3x - 1.
Để rèn luyện thêm kỹ năng giải bài tập về hàm số bậc nhất, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 1, hoặc tìm kiếm trên các trang web học toán online.
Bài 8 trang 82 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.