Chào mừng các em học sinh đến với lời giải chi tiết bài 38 trang 136 sách bài tập Toán 9 Cánh Diều tập 2. Bài học này tập trung vào việc ôn tập chương 4: Biến đổi phương trình tích.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
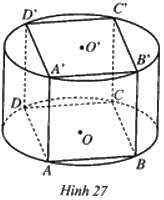
Cho hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a3. Hình trụ (T) có hai đáy là hai đường tròn (O), (O’) lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’ (Hình 27). Tính diện tích toàn phần của hình trụ (T) theo a.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a3. Hình trụ (T) có hai đáy là hai đường tròn (O), (O’) lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’ (Hình 27). Tính diện tích toàn phần của hình trụ (T) theo a.
Phương pháp giải - Xem chi tiết
Dựa vào: Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r(h + r)\).
Lời giải chi tiết
Do hình lập phương ABCD.A’B’C’D’ có thể tích bằng 27a3 nên cạnh hình lập phương là \(\sqrt[3]{{27{a^3}}} = 3a\).
Suy ra cạnh của hình vuông ABCD là 3a và bán kính của hình trụ bằng bán kính của đường tròn (O) ngoại tiếp hình vuông ABCD và bằng \(\frac{{3a\sqrt 2 }}{2}\).
Vậy diện tích toàn phần của hình trụ (T) là:
\(2\pi .\frac{{3a\sqrt 2 }}{2}.3a + 2\pi .{\left( {\frac{{3a\sqrt 2 }}{2}} \right)^2} = 9\pi {a^2}(\sqrt 2 + 1)\)
Bài 38 trang 136 sách bài tập Toán 9 Cánh Diều tập 2 là một bài tập ôn tập quan trọng, giúp học sinh củng cố kiến thức về biến đổi phương trình tích đã học trong chương 4. Bài tập này thường bao gồm các dạng bài tập như giải phương trình tích, tìm điều kiện xác định của phương trình, và ứng dụng các phương pháp biến đổi phương trình để giải quyết các bài toán thực tế.
Bài 38 thường bao gồm nhiều câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh áp dụng một kỹ năng hoặc kiến thức cụ thể. Các câu hỏi có thể liên quan đến:
Để giải bài tập 38 trang 136 SBT Toán 9 Cánh Diều tập 2 một cách hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Ví dụ: Giải phương trình (x - 2)(x + 3) = 0
Giải:
Phương trình (x - 2)(x + 3) = 0 tương đương với:
x - 2 = 0 hoặc x + 3 = 0
Nếu x - 2 = 0 thì x = 2
Nếu x + 3 = 0 thì x = -3
Vậy phương trình có hai nghiệm là x = 2 và x = -3
Giaitoan.edu.vn là một trang web học Toán 9 online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập chi tiết. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn khi giải bài 38 trang 136 sách bài tập Toán 9 Cánh Diều tập 2. Chúc các em học tập tốt!