Giải bài 41 trang 137 Sách bài tập Toán 9 - Cánh Diều tập 2

Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2

Giải bài 41 trang 137 Sách bài tập Toán 9 - Cánh Diều tập 2

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 41 trang 137 sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.

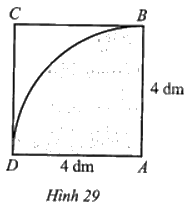
Từ một miếng tôn có dạng hình vuông ABCD cạnh 4 dm, người ta cắt ra một phần tư hình tròn tâm A bán kính AB = 4 dm (như phần được tô màu ở Hình 29) và cuộn lại thành một cái phễu hình nón. Tính chiều cao của cái phễu đó (theo đơn vị decimét và làm tròn kết quả đến hàng phần trăm).

Đề bài

Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2 1

Phương pháp giải - Xem chi tiết Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2 2

Dựa vào: Chu vi hình tròn \(2\pi R\).

Lời giải chi tiết

Chu vi của một phần tư hình tròn tâm A bán kính AB = 4 dm là:

\(\frac{1}{4}.2\pi .4 = 2\pi \) (dm).

Gọi R là bán kính đường tròn đáy của phễu.

Ta có 2πR = 2π nên R = 1 (dm).

Lại có, đường sinh của phễu là l = 4 dm, suy ra chiều cao của phễu là:

\(h = \sqrt {{l^2} - {r^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \approx 3,87\) (dm)

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 41 trang 137 sách bài tập toán 9 - Cánh diều tập 2 đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng toán học. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 41 trang 137 Sách bài tập Toán 9 - Cánh Diều tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 41 trang 137 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:

Hàm số bậc nhất: Định nghĩa, dạng tổng quát y = ax + b (a ≠ 0).
Hệ số a: Xác định tính chất đồng biến, nghịch biến của hàm số.
Đồ thị hàm số bậc nhất: Cách vẽ đồ thị, xác định giao điểm với các trục tọa độ.
Ứng dụng của hàm số bậc nhất: Giải các bài toán thực tế liên quan đến hàm số.

Nội dung bài 41 trang 137 Sách bài tập Toán 9 - Cánh Diều tập 2

Bài 41 yêu cầu học sinh giải các bài toán liên quan đến việc xác định hàm số bậc nhất, vẽ đồ thị và tìm các điểm đặc biệt trên đồ thị. Cụ thể, bài tập thường bao gồm:

Xác định hệ số a và b của hàm số y = ax + b khi biết các thông tin về đồ thị hoặc các điểm thuộc đồ thị.
Vẽ đồ thị của hàm số y = ax + b.
Tìm giao điểm của đồ thị hàm số với các trục tọa độ.
Giải các bài toán ứng dụng liên quan đến hàm số bậc nhất, ví dụ như bài toán về quãng đường, thời gian, tốc độ.

Hướng dẫn giải chi tiết bài 41 trang 137 Sách bài tập Toán 9 - Cánh Diều tập 2

Để giúp bạn giải bài tập này một cách dễ dàng, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng phần của bài tập. Dưới đây là một ví dụ minh họa:

Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định hệ số a và b, vẽ đồ thị và tìm giao điểm của đồ thị với trục Ox.

Giải:

Xác định hệ số a và b: So sánh hàm số y = 2x - 3 với dạng tổng quát y = ax + b, ta có a = 2 và b = -3.
Vẽ đồ thị: Để vẽ đồ thị, ta cần xác định hai điểm thuộc đồ thị. Ví dụ, ta có thể chọn x = 0 thì y = -3, và x = 1 thì y = -1. Vẽ hai điểm A(0; -3) và B(1; -1) lên mặt phẳng tọa độ và nối chúng lại, ta được đồ thị của hàm số y = 2x - 3.
Tìm giao điểm với trục Ox: Giao điểm của đồ thị với trục Ox là điểm có tung độ y = 0. Thay y = 0 vào phương trình hàm số, ta được 0 = 2x - 3, suy ra x = 3/2. Vậy giao điểm của đồ thị với trục Ox là điểm C(3/2; 0).

Mẹo giải bài tập hàm số bậc nhất

Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và ứng dụng của hàm số bậc nhất.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Sử dụng đồ thị: Vẽ đồ thị hàm số để trực quan hóa bài toán và tìm ra lời giải.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự và tài liệu tham khảo

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2 và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 9 để được hướng dẫn chi tiết hơn.

Kết luận

Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 41 trang 137 sách bài tập Toán 9 - Cánh Diều tập 2 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!