Bài 18 trang 107 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 18 trang 107 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
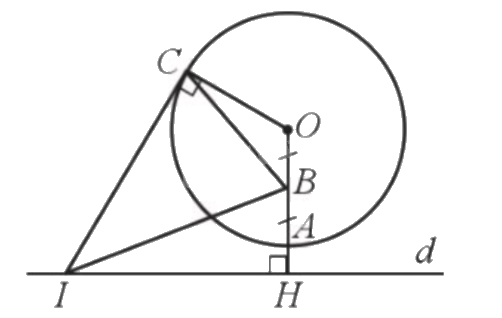
Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.
Đề bài
Cho đường tròn (O; 4 cm) và đường thẳng d sao cho khoảng cách từ điểm O đến đường thẳng d là OH = 5 cm. Đường thẳng OH cắt đường tròn (O) tại A. Gọi B là trung điểm của đoạn thẳng OA. Trên đường thẳng d, lấy một điểm I (khác H), kẻ tiếp tuyến IC của đường tròn (O) với C là tiếp điểm (Hình 17). Chứng minh tam giác IBC cân tại I.
Phương pháp giải - Xem chi tiết
Bước 1: Chứng minh \(I{B^2} = I{H^2} + B{H^2} = I{H^2} + 9\).
Bước 2: Chứng minh \(I{C^2} = I{O^2} - C{O^2} = O{H^2} + I{H^2} - C{O^2} = I{H^2} + 9\)
Lời giải chi tiết
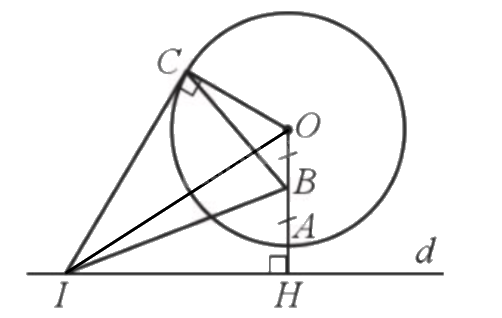
Kẻ OI.
Do B trung điểm của OA nên \(OB = BA = \frac{{OA}}{2} = \frac{4}{2} = 2\)cm.
Ta có \(HB = OH - OB = 5 - 2 = 3\)cm.
Xét tam giác vuông IBH có
\(I{B^2} = I{H^2} + B{H^2} = I{H^2} + 9\).
Xét tam giác vuông IOC có
\(I{C^2} = I{O^2} - C{O^2} = O{H^2} + I{H^2} - C{O^2} = {5^2} + I{H^2} - {4^2} = I{H^2} + 9\)
Suy ra \(I{B^2} = I{C^2}\left( { = I{H^2} + 9} \right)\), do đó \(IB = IC\), nên tam giác IBC cân tại B.
Bài 18 trang 107 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Để giải bài này, học sinh cần nắm vững các kiến thức về:
Dưới đây là lời giải chi tiết cho từng phần của bài 18:
Thông thường, phần này yêu cầu học sinh xác định hệ số góc của hàm số và vẽ đồ thị của hàm số đó. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Có thể chọn x = 0 để tìm y, hoặc chọn y = 0 để tìm x.
Ví dụ, nếu hàm số là y = 2x - 1:
Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị của hàm số y = 2x - 1.
Phần này yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để tìm giao điểm, học sinh cần giải hệ phương trình bậc nhất hai ẩn, trong đó mỗi phương trình biểu diễn một đường thẳng.
Ví dụ, tìm giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2:
Giải hệ phương trình:
Thay phương trình (2) vào phương trình (1), ta được:
-x + 2 = 2x - 1
3x = 3
x = 1
Thay x = 1 vào phương trình (2), ta được:
y = -1 + 2 = 1
Vậy giao điểm của hai đường thẳng là (1; 1).
Phần này thường yêu cầu học sinh sử dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, ví dụ như tính quãng đường đi được, tính tiền lương, tính giá thành sản phẩm,...
Để giải các bài toán này, học sinh cần:
Lưu ý:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 18 trang 107 sách bài tập Toán 9 Cánh diều tập 1 và tự tin giải các bài tập tương tự. Chúc các em học tốt!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Là hàm số có dạng y = ax + b, với a ≠ 0. |
| Hệ số góc | Là hệ số a trong hàm số y = ax + b. Nó cho biết độ dốc của đường thẳng. |