Giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi đã biên soạn lời giải bài 30 trang 116 một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng.

Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và \(\widehat {BAC} = 50^\circ \). So sánh các cung nhỏ AB, BC.

Đề bài

Cho đường tròn (O) và ba điểm A, B, C nằm trên đường tròn sao cho tam giác ABC cân tại A và \(\widehat {BAC} = 50^\circ \). So sánh các cung nhỏ AB, BC.

Phương pháp giải - Xem chi tiết Giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 1

Bước 1: Tính số đo góc B.

Bước 2: Tính số đo cung nhỏ AB và BC (số đo cung gấp 2 lần số đo góc nội tiếp chắn cung đó).

Lời giải chi tiết

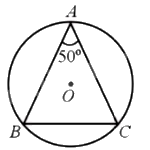
Giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 2

Do tam giác ABC cân tại A nên

\(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 50^\circ }}{2} = 65^\circ \).

Do đó số đo cung nhỏ AB là \(2.\widehat {ACB} = 65^\circ .2 = 130^\circ \)

Số đo cung nhỏ BC là \(2.\widehat A = 50^\circ .2 = 100^\circ \).

Vì \(130^\circ > 100^\circ \) nên cung nhỏ AB lớn hơn cung nhỏ BC.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 đặc sắc thuộc chuyên mục giải bài tập toán 9 trên nền tảng toán học. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1: Hướng dẫn chi tiết

Bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập chương 4: Hệ phương trình bậc hai hai ẩn. Bài tập này yêu cầu học sinh vận dụng kiến thức về phương pháp giải hệ phương trình bậc hai hai ẩn để giải các bài toán thực tế.

Nội dung bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1

Bài 30 bao gồm các dạng bài tập sau:

Dạng 1: Giải hệ phương trình bậc hai hai ẩn bằng phương pháp thế.
Dạng 2: Giải hệ phương trình bậc hai hai ẩn bằng phương pháp cộng đại số.
Dạng 3: Giải bài toán thực tế bằng cách lập hệ phương trình bậc hai hai ẩn.

Hướng dẫn giải chi tiết bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1

Để giúp bạn hiểu rõ hơn về cách giải bài 30 trang 116, chúng tôi sẽ trình bày chi tiết lời giải cho từng dạng bài tập.

Dạng 1: Giải hệ phương trình bậc hai hai ẩn bằng phương pháp thế

Ví dụ: Giải hệ phương trình sau:

{ x + y = 5

x^2 - y^2 = 15

Lời giải:

Từ phương trình x + y = 5, ta có y = 5 - x.
Thay y = 5 - x vào phương trình x^2 - y^2 = 15, ta được: x^2 - (5 - x)^2 = 15
Giải phương trình trên, ta tìm được x = 4 và x = -4.
Với x = 4, ta có y = 5 - 4 = 1.
Với x = -4, ta có y = 5 - (-4) = 9.
Vậy hệ phương trình có hai nghiệm: (4; 1) và (-4; 9).

Dạng 2: Giải hệ phương trình bậc hai hai ẩn bằng phương pháp cộng đại số

Ví dụ: Giải hệ phương trình sau:

{ 2x + y = 7

x^2 + y^2 = 25

Lời giải:

Từ phương trình 2x + y = 7, ta có y = 7 - 2x.
Thay y = 7 - 2x vào phương trình x^2 + y^2 = 25, ta được: x^2 + (7 - 2x)^2 = 25
Giải phương trình trên, ta tìm được x = 3 và x = -1.
Với x = 3, ta có y = 7 - 2(3) = 1.
Với x = -1, ta có y = 7 - 2(-1) = 9.
Vậy hệ phương trình có hai nghiệm: (3; 1) và (-1; 9).

Dạng 3: Giải bài toán thực tế bằng cách lập hệ phương trình bậc hai hai ẩn

Ví dụ: Một khu vườn hình chữ nhật có chu vi là 50m. Nếu tăng chiều dài thêm 5m và giảm chiều rộng đi 2m thì diện tích khu vườn tăng thêm 20m². Tính chiều dài và chiều rộng của khu vườn ban đầu.

Lời giải:

Gọi chiều dài của khu vườn là x (m) và chiều rộng là y (m).
Theo đề bài, ta có hệ phương trình sau:

{ 2(x + y) = 50

(x + 5)(y - 2) = xy + 20

Giải hệ phương trình trên, ta tìm được x = 15 và y = 10.
Vậy chiều dài của khu vườn là 15m và chiều rộng là 10m.

Lưu ý khi giải bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1

Nắm vững các phương pháp giải hệ phương trình bậc hai hai ẩn.
Đọc kỹ đề bài và xác định đúng các đại lượng cần tìm.
Kiểm tra lại kết quả sau khi giải.

Tổng kết

Bài 30 trang 116 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hệ phương trình bậc hai hai ẩn. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!