Bài 22 trang 109 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 22 trang 109 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho đường tròn (O; R) và điểm A nằm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O). a) Tính số đo góc MBN và độ dài đoạn thẳng BM theo R. b) Tứ giác AMON là hình gì ? Vì sao? c) Tính độ dài đoạn thẳng OH theo R với H là giao điểm của OA và MN.
Đề bài
Cho đường tròn (O; R) và điểm A nằm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O).
a) Tính số đo góc MBN và độ dài đoạn thẳng BM theo R.
b) Tứ giác AMON là hình gì ? Vì sao?
c) Tính độ dài đoạn thẳng OH theo R với H là giao điểm của OA và MN.
Phương pháp giải - Xem chi tiết
a) Áp dụng tỉ số lượng giác trong tam giác MBO để tính số đo góc MBO, từ đó tính được số đo góc MBN.
Tính BM: Áp dụng định lý Pythagore trong tam giác OBM.
b) Chứng minh 2 tam giác AMO và ANO đều.
c) Áp dụng tỉ số lượng giác trong tam giác MHO để tính OH.
Lời giải chi tiết
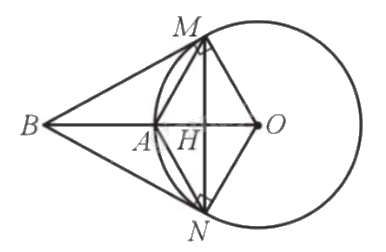
a) Ta có A là trung điểm của đoạn thẳng OB nên \(OB = 2OA = 2R\).
Do BM, BN là 2 tiếp tuyến của (O) nên \(MO \bot BM,NO \bot BN\) hay \(\widehat {BMO} = \widehat {BNO} = 90^\circ \) và \(\widehat {MBO} = \widehat {NBO} = \frac{{\widehat {MBN}}}{2}\); \(\widehat {MOB} = \widehat {NOB}\).
Xét tam giác MBO vuông tại M có
\(\sin \widehat {MBO} = \frac{{MO}}{{BO}} = \frac{R}{{2R}} = \frac{1}{2}\), do đó \(\widehat {MBO} = 30^\circ \).
Ta có \(\widehat {MBO} = \frac{{\widehat {MBN}}}{2}\) hay \(\widehat {MBN} = 2\widehat {MBO} = 2.30^\circ = 60^\circ \).
Áp dụng định lý Pythagore trong tam giác vuông OBM có:
\(BM = \sqrt {B{O^2} - M{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \)
b) Xét tam giác vuông MOB có \(\widehat {MBO} = 30^\circ \) nên \(\widehat {MOB} = 90^\circ - \widehat {MBO} = 90^\circ - 30^\circ = 60^\circ \)
Mà \(\widehat {MOB} = \widehat {NOB}\) nên \(\widehat {NOB} = 60^\circ \).
Xét tam giác AMO có \(AO = MO\left( { = R} \right)\) và \(\widehat {MOB} = 60^\circ \) nên tam giác AMO đều, suy ra \(AM = MO\).
Xét tam giác ANO có \(AO = NO\left( { = R} \right)\) và \(\widehat {NOB} = 60^\circ \) nên tam giác ANO đều, suy ra \(AN = NO\).
Mà \(OM = ON\left( { = R} \right)\) nên \(OM = ON = AM = AN\).
Vậy AMON là hình thoi.
c) Vì AMON là hình thoi nên 2 đường chéo AO và MN vuông góc với nhau.
Xét tam giác vuông MHO ta có:
\(\cos \widehat {MOH} = \frac{{OH}}{{MO}}\) hay \(OH = \cos \widehat {MOH}.MO = \cos 60^\circ .R = \frac{R}{2}\).
Bài 22 trang 109 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đường thẳng, hệ số góc, và mối quan hệ giữa các đường thẳng (song song, vuông góc).
Bài 22 thường bao gồm các dạng bài tập sau:
Để giải bài 22 trang 109 sách bài tập Toán 9 Cánh diều tập 1, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử đề bài yêu cầu tìm hệ số góc của đường thẳng có phương trình y = 2x + 3. Ta có thể xác định hệ số góc bằng cách so sánh phương trình với dạng tổng quát y = ax + b, trong đó a là hệ số góc. Trong trường hợp này, a = 2, vậy hệ số góc của đường thẳng là 2.
Dạng 1: Xác định hệ số góc
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b. Hệ số a chính là hệ số góc của đường thẳng.
Dạng 2: Viết phương trình đường thẳng
Để viết phương trình đường thẳng khi biết hệ số góc và một điểm thuộc đường thẳng, ta sử dụng công thức y - y0 = a(x - x0), trong đó (x0, y0) là tọa độ của điểm thuộc đường thẳng và a là hệ số góc.
Dạng 3: Xác định điều kiện song song, vuông góc
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2. Hai đường thẳng vuông góc khi và chỉ khi a1 * a2 = -1.
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
Bài 22 trang 109 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, các em có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.