Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 9 Cánh Diều tập 2. Bài viết này sẽ hướng dẫn bạn giải bài 40 trang 137 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
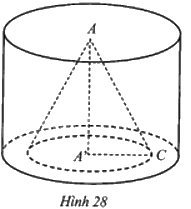
Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy (A'C = frac{2}{3}R) và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?
Đề bài
Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy \(A'C = \frac{2}{3}R\)và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích hình trụ: \(V = \pi {r^2}h\).
Thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
Thể tích của khối gỗ hình trụ (T) là: πR2h.
Thể tích của khối gỗ hình nón (N) là: \(\frac{1}{3}\pi .{\left( {\frac{2}{3}R} \right)^2}.h = \frac{4}{{27}}\pi {R^2}h\).
Thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối gỗ hình nón (N) là
\(\pi {R^2}h - \frac{4}{{27}}\pi {R^2}h = \frac{{23}}{{27}}\pi {R^2}h\).
Tỉ số phần trăm của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) so với thể tích của khối gỗ (T) ban đầu là \(\frac{{\frac{{23}}{{27}}\pi {R^2}h}}{{\pi {R^2}h}}.100\% \approx 85,2\% \).
Vậy thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng khoảng 85,2% thể tích của khối gỗ (T) ban đầu.
Bài 40 trang 137 sách bài tập Toán 9 Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 40 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 40, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập. Lưu ý rằng, đây chỉ là một trong nhiều cách giải bài tập. Bạn có thể tìm tòi và khám phá các phương pháp giải khác nhau để nâng cao kỹ năng giải toán của mình.
Câu hỏi: Tìm hệ số a và b của hàm số y = ax + b, biết rằng đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải:
Vì đồ thị của hàm số đi qua điểm A(1; 2), ta có: 2 = a * 1 + b => a + b = 2 (1)
Vì đồ thị của hàm số đi qua điểm B(-1; 0), ta có: 0 = a * (-1) + b => -a + b = 0 (2)
Từ (1) và (2), ta có hệ phương trình:
| a | b |
|---|---|
| 1 | 1 |
| -1 | 1 |
Giải hệ phương trình này, ta được: a = 1 và b = 1.
Vậy, hàm số cần tìm là y = x + 1.
Bài 40 trang 137 SBT Toán 9 Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng, với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn khi giải các bài tập tương tự.
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!