Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 6 trang 53 sách bài tập Toán 9 - Cánh Diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho hình thang cân ABCD có AB // CD và \(AC \bot AD\). Tính độ dài cạnh AD, biết \(AB = 5cm,CD = 11cm.\)
Đề bài
Cho hình thang cân ABCD có AB // CD và \(AC \bot AD\). Tính độ dài cạnh AD, biết \(AB = 5cm,CD = 11cm.\)
Phương pháp giải - Xem chi tiết
Bước 1: Kẻ đường cao BH, CK.
Bước 2: Chứng minh ABKH là hình chữ nhật, từ đó tính được HK.
Bước 3: Chứng minh \(\Delta AHD = \Delta AKC\), từ đó tính được DH.
Bước 4: Chứng minh , từ đó tính được AD.
Lời giải chi tiết
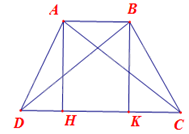
Kẻ BH, CK lần lượt vuông góc với CD tại H, K do đó \(\widehat {AHK} = \widehat {BKH} = 90^\circ .\)
Do \(BK \bot CD,AB//CD\) nên \(BK \bot AB\), suy ra \(\widehat {ABK} = 90^\circ \).
Xét tứ giác ABKH, ta có \(\widehat {AHK} = \widehat {BKH} = \widehat {ABK} = 90^\circ \) nên ABKH là hình chữ nhật.
Suy ra \(HK = AB = 5cm.\)
Xét tam giác AHD và tam giác BKC ta có:
AD = BC (ABCD là hình thang cân)
AH = BK (ABKH là hình chữ nhật)
\(\widehat {AHD} = \widehat {BKC}\left( { = 90^\circ } \right)\)
Do đó \(\Delta AHD = \Delta AKC\)(cạnh huyền – cạnh góc vuông)
Nên \(HD = KC = \frac{{CD - HK}}{2} = 3cm.\)
Xét tam giác ACD và tam giác HAD có:
\(\widehat {ADC}\) chung, \(\widehat {DAC} = \widehat {AHD}( = 90^\circ )\)
Suy ra nên \(\frac{{CD}}{{AD}} = \frac{{AD}}{{HD}}\) hay \(A{D^2} = CD.HD\),
do đó \(AD = \sqrt {CD.HD} = \sqrt {11.3} = \sqrt {33} cm.\)
Bài 6 trang 53 sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 6 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 6 trang 53 sách bài tập Toán 9 - Cánh Diều tập 1, học sinh cần nắm vững các kiến thức sau:
Câu a: Xác định hệ số góc của đường thẳng y = -2x + 3.
Hệ số góc của đường thẳng y = -2x + 3 là a = -2.
Câu b: Xác định hệ số góc của đường thẳng đi qua hai điểm A(1; 2) và B(3; 6).
Hệ số góc của đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2) được tính theo công thức:
a = (y2 - y1) / (x2 - x1)
Thay x1 = 1, y1 = 2, x2 = 3, y2 = 6 vào công thức, ta được:
a = (6 - 2) / (3 - 1) = 4 / 2 = 2
Vậy hệ số góc của đường thẳng đi qua hai điểm A(1; 2) và B(3; 6) là 2.
Câu c: Tìm m để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x - 1.
Để hai đường thẳng song song, hệ số góc của chúng phải bằng nhau. Do đó, ta có:
m - 1 = 3
m = 4
Vậy m = 4 để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x - 1.
Câu d: Tìm m để đường thẳng y = (2m + 1)x - 3 vuông góc với đường thẳng y = -x + 5.
Để hai đường thẳng vuông góc, tích hệ số góc của chúng phải bằng -1. Do đó, ta có:
(2m + 1) * (-1) = -1
2m + 1 = 1
2m = 0
m = 0
Vậy m = 0 để đường thẳng y = (2m + 1)x - 3 vuông góc với đường thẳng y = -x + 5.
Để củng cố kiến thức về hàm số bậc nhất và các điều kiện song song, vuông góc, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 1 và các nguồn tài liệu học tập khác.
Bài 6 trang 53 sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, bạn sẽ tự tin hơn khi giải các bài tập tương tự.