Bài 43 trang 74 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 43 trang 74 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
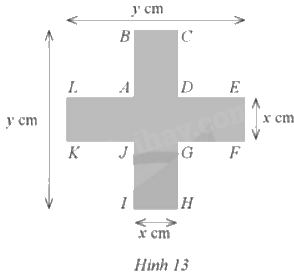
Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và (y = x + 25,AL = AB = CD = DE = FG = GH = IJ = JK)như hình 13. a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x. b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2.
Đề bài
Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và \(y = x + 25,\) \(AL = AB = CD = DE = FG = GH = IJ = JK\) như hình 13.
a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x.
b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2.
Phương pháp giải - Xem chi tiết
a) Diện tích cần tìm = diện tích BCHI + diện tích LEFK - diện tích ADGJ
b) Bước 1: Lập phương trình thể hiện diện tích phần hình chữ thập.
Bước 2: Giải phương trình, đối chiếu điều kiện và kết luận.
Lời giải chi tiết
Điều kiện \(x > 0;y > 25\).
a) Diện tích hình chữ nhật BCHI là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2)
Diện tích hình chữ nhật LEFK là \(xy = x\left( {x + 25} \right) = {x^2} + 25x\) (m2)
Diện tích hình vuông ADGJ là \({x^2}\) (m2)
Diện tích phần hình chữ thập là: \({x^2} + 25x + {x^2} + 25x - {x^2} = {x^2} + 50x\)(m2)
b) Vì diện tích phần hình chữ thập của biển báo giao thông đó là 975cm2 nên ta có:
\({x^2} + 50x = 975\), do đó \({x^2} + 50x - 975 = 0\)
Ta có \(\Delta ' = {25^2} - 1.\left( { - 975} \right) = 1600 > 0\) nên phương trình có 2 nghiệm phân biệt:
\({x_1} = \frac{{ - 25 - \sqrt {1600} }}{1} = - 65;{x_2} = \frac{{ - 25 + \sqrt {1600} }}{1} = 15\)
Ta thấy \({x_1} = - 65\) không thỏa mãn điều kiện; \({x_2} = 15\) thỏa mãn điều kiện.
Vậy \(x = 15\).
Bài 43 trang 74 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Bài 43 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 43. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm từng bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Cho hàm số y = ax + b. Biết rằng đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0). Hãy tìm a và b.
Giải:
Vì đồ thị của hàm số đi qua điểm A(1; 2) nên ta có:
2 = a * 1 + b => a + b = 2 (1)
Vì đồ thị của hàm số đi qua điểm B(-1; 0) nên ta có:
0 = a * (-1) + b => -a + b = 0 (2)
Cộng (1) và (2) ta được:
2b = 2 => b = 1
Thay b = 1 vào (1) ta được:
a + 1 = 2 => a = 1
Vậy hàm số cần tìm là y = x + 1.
Ngoài bài 43, các em có thể gặp các bài tập tương tự với các yêu cầu khác nhau. Để giải các bài tập này, các em cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2, hoặc trên các trang web học toán online uy tín.
Bài 43 trang 74 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.