Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 125 sách bài tập Toán 9 - Cánh diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các lời giải chuẩn xác và đầy đủ.
Bác An cần đúc một ống cống thoát nước bằng bê tông có dạng hình trụ rỗng với đường kính đường tròn đáy ngoài là 0,8 m, chiều dài ống là 1,5 m và bề dày là 0,1 m (Hình 7). Hỏi số tiền bác An cần dùng để làm được một ống cống như thế là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)? Biết giá loại bê tông bác An sử dụng là 1 000 000 đồng một mét khối.
Đề bài
Bác An cần đúc một ống cống thoát nước bằng bê tông có dạng hình trụ rỗng với đường kính đường tròn đáy ngoài là 0,8 m, chiều dài ống là 1,5 m và bề dày là 0,1 m (Hình 7).
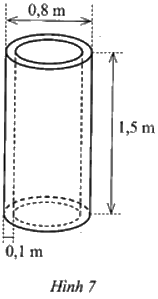
Hỏi số tiền bác An cần dùng để làm được một ống cống như thế là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)? Biết giá loại bê tông bác An sử dụng là 1 000 000 đồng một mét khối.
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích hình trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết
Bán kính đáy của hình trụ bên ngoài là: 0,8 : 2 = 0,4 (m).
Hình trụ (bên ngoài) với bán kính đáy 0,4 m, chiều cao 1,5 m có thể tích là:
πr2h = π . (0,4)2 . 1,5 = 0,24π (m3).
Do bề dày của ống cống là 0,1 m nên đường kính đường tròn đáy của hình trụ (bên trong) là: 0,8 – 0,1 – 0,1 = 0,6 (m).
Bán kính đáy của hình trụ bên trong là: 0,6 : 2 = 0,3 (m).
Hình trụ (bên trong) với bán kính đáy 0,3 m, chiều cao 1,5 m có thể tích là:
πr2h = π . (0,3)2 . 1,5 = 0,135π (m3).
Lượng bê tông cần dùng để đúc ống cống đó là:
0,24π – 0,135π = 0,105π (m3).
Số tiền bác An cần dùng để làm được một ống cống như yêu cầu là:
0,105π . 1 000 000 = 105 000π ≈ 105 000.3,14 = 329 700 ≈ 330 000 (đồng).
Bài 8 trang 125 sách bài tập Toán 9 - Cánh diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, liên quan đến việc xác định hàm số, vẽ đồ thị hàm số và ứng dụng hàm số vào việc giải quyết các bài toán hình học.
Bài 8 bao gồm các phần chính sau:
Để giải câu a, ta cần xác định hàm số bậc nhất đi qua hai điểm A(0; 2) và B(2; 6).
Gọi hàm số có dạng y = ax + b. Thay tọa độ điểm A vào hàm số, ta được:
2 = a * 0 + b => b = 2
Thay tọa độ điểm B vào hàm số, ta được:
6 = a * 2 + 2 => 2a = 4 => a = 2
Vậy hàm số cần tìm là y = 2x + 2.
Để vẽ đồ thị hàm số y = 2x + 2, ta xác định hai điểm thuộc đồ thị, ví dụ:
Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x + 2.
Để tìm giao điểm của đồ thị hàm số y = 2x + 2 với đường thẳng y = -x + 5, ta giải hệ phương trình:
{ y = 2x + 2y = -x + 5 }
Thay y = 2x + 2 vào phương trình thứ hai, ta được:
2x + 2 = -x + 5 => 3x = 3 => x = 1
Thay x = 1 vào phương trình y = 2x + 2, ta được:
y = 2 * 1 + 2 = 4
Vậy giao điểm của hai đường thẳng là (1; 4).
Để hiểu rõ hơn về hàm số bậc nhất, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Cánh diều tập 2. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học toán online để nâng cao kiến thức và kỹ năng giải bài tập.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải bài 8 trang 125 sách bài tập Toán 9 - Cánh diều tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!