Bài 10 trang 37 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 37 Sách bài tập Toán 9 - Cánh Diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn (frac{{AB.BC + AD.DC}}{2}.)
Đề bài
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)
Phương pháp giải - Xem chi tiết
Kẻ đường cao CH và AK.
Tính diện tích tam giác ABC và ACD.
Do đó\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} = \frac{{AB.CH + DC.AK}}{2}\)
Kết hợp với điều kiện \(CH \le BC,AK \le AD\), ta được điều phải chứng minh.
Lời giải chi tiết
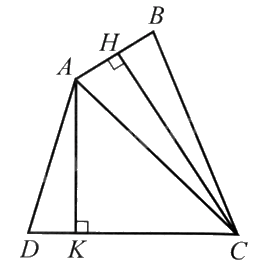
Kẻ \(CH \bot AB,AK \bot DC(H \in AB,K \in DC)\).
Ta có \({S_{ABC}} = \frac{{AB.CH}}{2},{S_{ACD}} = \frac{{DC.AK}}{2}\)
Do đó
\({S_{ABCD}} = {S_{ABC}} + {S_{ACD}} \\= \frac{{AB.CH}}{2} + \frac{{DC.AK}}{2} = \frac{{AB.CH + DC.AK}}{2}\)
Mà \(CH \le BC,AK \le AD\) suy ra \({S_{ABCD}} \le \frac{{AB.BC + AD.DC}}{2}\)
Vậy diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB.BC + AD.DC}}{2}.\)
Bài 10 trang 37 Sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc và tung độ gốc của hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Bài 10 thường bao gồm các dạng bài tập sau:
Để giải bài 10 trang 37 Sách bài tập Toán 9 - Cánh Diều tập 1, các em cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 10 trang 37:
Ví dụ: Cho đồ thị hàm số đi qua hai điểm A(0; 2) và B(1; 4). Hãy xác định hàm số bậc nhất có dạng y = ax + b.
Lời giải:
Thay tọa độ điểm A(0; 2) vào phương trình y = ax + b, ta được: 2 = a * 0 + b => b = 2.
Thay tọa độ điểm B(1; 4) vào phương trình y = ax + b, ta được: 4 = a * 1 + 2 => a = 2.
Vậy hàm số bậc nhất cần tìm là y = 2x + 2.
Ví dụ: Vẽ đồ thị hàm số y = -x + 1.
Lời giải:
Xác định hai điểm thuộc đồ thị:
Nối hai điểm A(0; 1) và B(1; 0) lại với nhau, ta được đồ thị hàm số y = -x + 1.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian.
Lời giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km).
Hàm số biểu thị quãng đường đi được của người đó theo thời gian là y = 15x.
Bài 10 trang 37 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin giải quyết bài tập này một cách hiệu quả.