Bài 25 trang 109 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 25 trang 109 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A với \(R \ne r\). Đường nối OO' lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O') tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh: a) \(\widehat {DME} = 90^\circ \) b) MA tiếp xúc với hai đường tròn (O) và (O') c) MD. MB=ME. MC
Đề bài
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A với \(R \ne r\). Đường nối OO' lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O') tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh:
a) \(\widehat {DME} = 90^\circ \)
b) MA tiếp xúc với hai đường tròn (O) và (O')
c) MD. MB = ME. MC
Phương pháp giải - Xem chi tiết
a) Bước 1: Chứng minh \(\widehat {BOD} = \widehat {AO'E}\).
Bước 2: Chứng minh \(\widehat B = \widehat {EAO'} = \frac{{180^\circ - \widehat {EO'A}}}{2}\).
Bước 3: Chứng minh \(\widehat C + \widehat B = 90^\circ \).
b) Bước 1: Chứng minh \(IA = ID\).
Bước 2: Chứng minh \(\Delta OAI = \Delta ODI\).
c) Chứng minh tam giác BCM đồng dạng với tam giác EDM.
Lời giải chi tiết
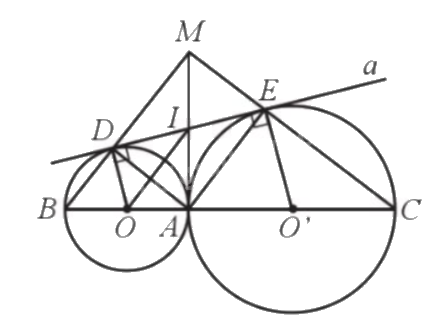
a) Ta có DE tiếp xúc với (O) và (O’) nên \(DO \bot DE,EO' \bot DE\), do đó \(DO//EO'\),
Suy ra \(\widehat {BOD} = \widehat {AO'E}\) (2 góc so le trong). (1)
Do \(BO = DO\left( { = R} \right)\) nên tam giác BOD cân tại O, do đó \(\widehat B = \frac{{180^\circ - \widehat {BOD}}}{2}\). (2)
Do \(AO' = EO'\left( { = r} \right)\) nên tam giác AO’E cân tại O’, do đó \(\widehat {EAO'} = \frac{{180^\circ - \widehat {EO'A}}}{2}\). (3)
Từ (1), (2), (3) suy ra \(\widehat B = \widehat {EAO'}\). (4)
Xét tam giác EAC có nên tam giác EAC vuông tại E, do đó \(\widehat C + \widehat {EAO'} = 90^\circ \) (5)
Từ (4) và (5) suy ra \(\widehat C + \widehat B = 90^\circ \).
Xét tam giác MBC có \(\widehat C + \widehat B + \widehat {BMC} = 180^\circ \) hay \(90^\circ + \widehat {BMC} = 180^\circ \). Vậy \(\widehat {BMC} = 90^\circ \) hay \(\widehat {DME} = 90^\circ \).
b) Xét tam giác BDA có \(OB = OA = OD = \frac{{AB}}{2}\) nên tam giác BDA vuông tại D hay \(\widehat {BDA} = 90^\circ \), do đó \(\widehat {ADM} = 90^\circ \).
Xét tam giác AEC có \(O'E = O'A = O'C = \frac{{AC}}{2}\) nên tam giác AEC vuông tại E
hay \(\widehat {AEC} = 90^\circ \), do đó \(\widehat {AEM} = 90^\circ \).
Xét tứ giác DMEA có \(\widehat {ADM} = \widehat {DME} = \widehat {MEA} = 90^\circ \) suy ra DMEA là hình chữ nhật,
nên \(IA = ID\).
Xét 2 tam giác OAI và ODI có:
OI chung; \(OD = OA\left( { = R} \right)\); \(IA = ID\)
Suy ra \(\Delta OAI = \Delta ODI\) (c.c.c), do đó \(\widehat {OAI} = \widehat {ODI} = 90^\circ \) hay MA vuông góc với BD tại A.
Vậy MA tiếp xúc với hai đường tròn (O) và (O').
c) Do MA tiếp xúc với hai đường tròn (O) nên MA là tiếp tuyến của (O) hay \(\widehat {BAM} = \widehat {IAD} + \widehat {DAB} = 90^\circ \).
Ta lại có: tam giác ADB cân tại D nên \(\widehat B + \widehat {DAB} = 90^\circ \), do đó \(\widehat B = \widehat {IAD}\).
Mặt khác \(\widehat {MED} = \widehat {IAD}\) (DMEA là hình chữ nhật), do đó \(\widehat {MED} = \widehat B\).
Xét 2 tam giác BCM và EDM có:
\(\widehat {MED} = \widehat B\);
\(\widehat {BMC} = 90^\circ \)
Suy ra \(\Delta BCM\backsim \Delta EDM\) (g.g), nên \(\frac{{MD}}{{EM}} = \frac{{MC}}{{MD}}\) hay \(MD.MB = ME.MC\).
Bài 25 trang 109 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Để giải bài tập này hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 25 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập.
Hàm số y = 2x - 3 là hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Vậy, hệ số góc của hàm số y = 2x - 3 là a = 2.
Để vẽ đồ thị hàm số y = -x + 1, ta thực hiện các bước sau:
Ví dụ bảng giá trị:
| x | y |
|---|---|
| 0 | 1 |
| 1 | 0 |
| -1 | 2 |
Để tìm tọa độ giao điểm của hai đường thẳng y = x + 2 và y = -2x + 5, ta giải hệ phương trình sau:
{ y = x + 2, y = -2x + 5 }
Thay y = x + 2 vào phương trình y = -2x + 5, ta được:
x + 2 = -2x + 5
3x = 3
x = 1
Thay x = 1 vào phương trình y = x + 2, ta được:
y = 1 + 2 = 3
Vậy, tọa độ giao điểm của hai đường thẳng y = x + 2 và y = -2x + 5 là (1, 3).
Bài 25 trang 109 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.