Bài 16 trang 85 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 16 trang 85 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
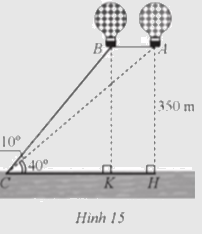
Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được \(\widehat {ACH} = 40^\circ ,\widehat {ACB} = 10^\circ \) (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).
Đề bài
Hai khinh khí cầu được thả lên cùng độ cao là 350 m (ở hai vị trí A và B). Tại vị trí C trên mặt đất, người ta quan sát và đo được \(\widehat {ACH} = 40^\circ ,\widehat {ACB} = 10^\circ \) (Hình 15). Tính khoảng cách giữa hai khinh khí cầu (làm tròn kết quả đến hàng đơn vị của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng hệ thức lượng để tính CK, CH.
Bước 2: AB = KH = CH – CK.
Lời giải chi tiết
Xét tam giác vuông ACH ta có \(\tan \widehat {ACH} = \frac{{AH}}{{CH}}\) hay \(CH = \frac{{AH}}{{\tan \widehat {ACH}}} = \frac{{350}}{{\tan 40^\circ }}.\)
Ta có \(\widehat {BCK} = \widehat {BCA} + \widehat {ACH} = 10^\circ + 40^\circ = 50^\circ \)
Xét tam giác vuông BCK ta có \(\tan \widehat {BCK} = \frac{{BK}}{{CK}}\) hay \(CK = \frac{{BK}}{{\tan \widehat {BCK}}} = \frac{{350}}{{\tan 50^\circ }}.\)
\(KH = CH - CK = \frac{{350}}{{\tan 40^\circ }} - \frac{{350}}{{\tan 50^\circ }} \approx 123\)m.
Mà \(KH = AB\) nên \(AB \approx 123\)m.
Vậy khoảng cách giữa hai khinh khí cầu khoảng 123m.
Bài 16 trang 85 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó 'a' là hệ số góc. Ví dụ, nếu phương trình đường thẳng là 2x + 3y = 6, ta sẽ biến đổi về dạng y = (-2/3)x + 2. Vậy hệ số góc của đường thẳng này là -2/3.
Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc. Do đó, để tìm đường thẳng song song với đường thẳng y = ax + b, ta chỉ cần chọn một hệ số góc khác 'b' và giữ nguyên hệ số góc 'a'. Ví dụ, đường thẳng y = 2x + 1 song song với đường thẳng y = 2x - 3.
Hai đường thẳng vuông góc khi và chỉ khi tích của hệ số góc của chúng bằng -1. Do đó, nếu đường thẳng có hệ số góc 'a', thì đường thẳng vuông góc với nó sẽ có hệ số góc -1/a. Ví dụ, đường thẳng y = 3x + 2 vuông góc với đường thẳng y = (-1/3)x + 5.
Giả sử đề bài yêu cầu tìm hệ số góc của đường thẳng 4x - y = 8. Ta biến đổi phương trình về dạng y = 4x - 8. Vậy hệ số góc của đường thẳng này là 4.
Tiếp theo, hãy tìm đường thẳng song song với đường thẳng y = -x + 1. Đường thẳng song song có dạng y = -x + c (với c khác 1). Ví dụ, y = -x + 5 là một đường thẳng song song.
Cuối cùng, tìm đường thẳng vuông góc với đường thẳng y = 2x - 3. Hệ số góc của đường thẳng này là 2, vậy hệ số góc của đường thẳng vuông góc là -1/2. Đường thẳng vuông góc có dạng y = (-1/2)x + d (với d là một số thực bất kỳ).
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 1. Hãy chú ý phân tích đề bài, xác định đúng các yếu tố cần tìm và áp dụng các công thức, định lý đã học.
Bài 16 trang 85 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh nắm vững kiến thức về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Công thức |
|---|---|
| Hệ số góc | a trong phương trình y = ax + b |
| Đường thẳng song song | a1 = a2 |
| Đường thẳng vuông góc | a1 * a2 = -1 |