Bài 28 trang 61 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 28 trang 61 Sách bài tập Toán 9 - Cánh Diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
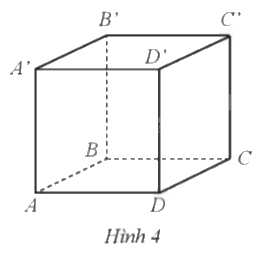
Một chất điểm di chuyển từ định A' đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?
Đề bài
Một chất điểm di chuyển từ định A' đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?
Phương pháp giải - Xem chi tiết
Phân tích: Quãng đường ngắn nhất mà chất điểm đó di chuyểnlà đi thẳng theo đoạn thẳng A’C.
Tính A’C: Dựa vào định lý Pythagore trong tam giác vuông AA’C.
Lời giải chi tiết
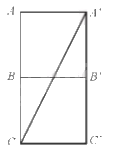
Giả sử chất điểm đó đi qua các mặt ABB’A’ và BCC’B’ của hình lập phương (các mặt khác tương tự). Trên đây là hình triển khai của các mặt ABB’A’ và BCC’B.
Tam giác AA’C vuông tại A nên áp dụng định lý Pythagore ta có:
\(A'{C^2} = AA{'^2} + A{C^2} = AA{'^2} + {\left( {AB + BC} \right)^2} = {1^2} + {\left( {1 + 1} \right)^2} = 5\)
Do đó \(A'C = \sqrt 5 dm\).
Vậy quãng đường ngắn nhất mà chất điểm đó di chuyển là \(\sqrt 5 dm.\)
Bài 28 thuộc chương trình Sách bài tập Toán 9 - Cánh Diều tập 1, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán liên quan đến thực tế. Bài tập này thường yêu cầu học sinh xác định hàm số, tìm điểm thuộc đồ thị hàm số, và giải các bài toán liên quan đến sự thay đổi của hàm số.
Bài 28 bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 28 trang 61 Sách bài tập Toán 9 - Cánh Diều tập 1, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Đề bài: ... (Nội dung đề bài cụ thể)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Đề bài: ... (Nội dung đề bài cụ thể)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Đề bài: ... (Nội dung đề bài cụ thể)
Lời giải: ... (Lời giải chi tiết, bao gồm các bước giải và giải thích rõ ràng)
Để giải quyết hiệu quả bài 28 trang 61 Sách bài tập Toán 9 - Cánh Diều tập 1, các em cần nắm vững các kiến thức sau:
Dưới đây là một số mẹo giúp các em giải bài tập hàm số hiệu quả hơn:
Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 28 trang 61 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các kiến thức bổ ích mà chúng tôi cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.