Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 27 trang 115 sách bài tập Toán 9 - Cánh Diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
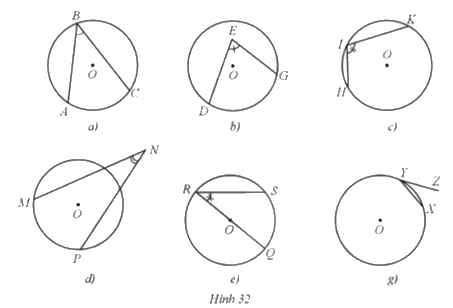
Trong các góc \(ABC,DEG,HIK,MNP,QRS,XYZ\) lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp, vì sao?
Đề bài
Trong các góc \(ABC,DEG,HIK,MNP,QRS,XYZ\) lần lượt ở các hình 32a, 32b, 32c, 32d, 32e, 32g, góc nào là góc nội tiếp, vì sao?
Phương pháp giải - Xem chi tiết
Góc nội tiếp: Góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung.
Lời giải chi tiết
Các góc ABC, HIK, QRS là các góc nội tiếp vì các góc này có đỉnh nằm trên đường tròn và hai cạnh chứa 2 dây cung của đường tròn.
Bài 27 trang 115 sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến việc xác định hàm số, tìm điểm thuộc đồ thị hàm số và ứng dụng hàm số vào các bài toán hình học.
Bài 27 bao gồm các câu hỏi và bài tập sau:
Để xác định hệ số a, ta thay tọa độ điểm A(1; 5) vào phương trình hàm số y = ax + 3:
5 = a * 1 + 3
=> a = 5 - 3 = 2
Vậy, hệ số a của hàm số là 2.
Để tìm giá trị của x, ta thay y = 7 vào phương trình hàm số y = 2x - 1:
7 = 2x - 1
=> 2x = 7 + 1 = 8
=> x = 8 / 2 = 4
Vậy, giá trị của x là 4.
Để vẽ đồ thị của hàm số y = -x + 2, ta thực hiện các bước sau:
Công thức tính quãng đường đi được (s) theo thời gian (t) là:
s = v * t
Trong đó:
Với vận tốc v = 15 km/h, công thức tính quãng đường đi được là:
s = 15t
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 27 trang 115 sách bài tập Toán 9 - Cánh Diều tập 1. Chúc bạn học tập tốt!