Bài 17 trang 112 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 17 trang 112 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
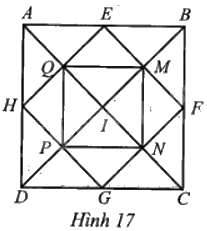
Cho hình vuông ABCD, I là giao điểm của hai đường chéo AC, BD. E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Q, N lần lượt là giao điểm của AC với HE và AC với GF; M, P lần lượt là giao điểm của BD với EF và BD với GH (Hình 17). Phép quay thuận chiều 90° tâm I có giữ nguyên các tứ giác EFGH và tứ giác MNPQ hay không? Vì sao?
Đề bài
Cho hình vuông ABCD, I là giao điểm của hai đường chéo AC, BD. E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Q, N lần lượt là giao điểm của AC với HE và AC với GF; M, P lần lượt là giao điểm của BD với EF và BD với GH (Hình 17). Phép quay thuận chiều 90° tâm I có giữ nguyên các tứ giác EFGH và tứ giác MNPQ hay không? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên.
Lời giải chi tiết
Vì I là giao điểm của hai đường chéo AC, BD của hình vuông ABCD nên I là trung điểm của AC và BD.
Vì E, I lần lượt là trung điểm các cạnh AB, AC nên EI là đường trung bình của ∆ABC.
Suy ra EI // BC và \(EI = \frac{1}{2}BC\).
Chứng minh tương tự, ta cũng có IG là đường trung bình của ∆BCD. Suy ra IG // BC và \(IG = \frac{1}{2}BC\).
Do đó IE // BC // IG và IE = IG.
Theo tiên đề Euclid, qua I có hai đường thẳng IE và IG cùng song song với BC nên ba điểm E, I, G thẳng hàng. Lại có IE = IG nên I là trung điểm của EG.
Chứng minh tương tự ta cũng có I là trung điểm của HF.
Do đó tứ giác EFGH là hình bình hành.
Ta có I là trung điểm của EG và HF nên EG = 2EI và HF = 2IF.
Mà BC = 2EI, CD = 2IF và BC = CD (do ABCD là hình vuông) nên EG = HF.
Do đó hình bình hành EFGH là hình chữ nhật.
Mặt khác, IE // BC, IF // CD và BC ⊥ CD nên IE ⊥ IF hay EG ⊥ HF.
Suy ra hình chữ nhật EFGH là hình vuông và I là giao điểm hai đường chéo.
Như vậy, phép quay thuận chiều 90° tâm I giữ nguyên hình vuông EFGH.
⦁ Ta có E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác, do đó EF // AC hay EM // AI.
Xét ∆ABI có E là trung điểm của AB và EM // AI nên EM là đường trung bình của tam giác, do đó M là trung điểm của BI, nên \(MI = \frac{1}{2}BI\) mà IB = ID = \(\frac{1}{2}BD\).
Nên \(IM = \frac{1}{4}BD\).
Chứng minh tương tự ta có IM = IP = \(\frac{1}{4}BD\); IN = IQ = \(\frac{1}{4}AC\).
Mà AC = BD nên IM = IN = IP = IQ và MP = NQ.
Do đó MNPQ là hình chữ nhật, lại có MP ⊥ NQ (do AC ⊥ BD) nên hình chữ nhật MNPQ là hình vuông có I là giao điểm hai đường chéo.
Như vậy, phép quay thuận chiều 90° tâm I giữ nguyên hình vuông MNPQ.
Vậy phép quay thuận chiều 90° tâm I giữ nguyên các tứ giác EFGH và MNPQ.
Bài 17 trang 112 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập thường bao gồm các bước sau:
Bài 17: Cho hàm số y = 2x + 3.
(a) Vẽ đồ thị của hàm số.
Để vẽ đồ thị của hàm số y = 2x + 3, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = 2(0) + 3 = 3. Vậy điểm A(0; 3) thuộc đồ thị. Chọn x = 1, ta có y = 2(1) + 3 = 5. Vậy điểm B(1; 5) thuộc đồ thị.
Vẽ đường thẳng đi qua hai điểm A(0; 3) và B(1; 5), ta được đồ thị của hàm số y = 2x + 3.
(b) Tìm tọa độ giao điểm của đồ thị hàm số với đường thẳng y = -x + 6.
Để tìm tọa độ giao điểm của hai đường thẳng y = 2x + 3 và y = -x + 6, ta giải hệ phương trình:
{ y = 2x + 3 y = -x + 6 }
Thay y = 2x + 3 vào phương trình y = -x + 6, ta được:
2x + 3 = -x + 6
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 3, ta được:
y = 2(1) + 3 = 5
Vậy tọa độ giao điểm của hai đường thẳng là (1; 5).
(c) Tìm các điểm M(x; y) thuộc đồ thị hàm số y = 2x + 3 sao cho M cách đều hai điểm A(1; 2) và B(-1; 4).
Gọi M(x; y) là điểm thuộc đồ thị hàm số y = 2x + 3. Ta có MA = MB.
MA2 = (x - 1)2 + (y - 2)2
MB2 = (x + 1)2 + (y - 4)2
Vì MA = MB nên MA2 = MB2.
(x - 1)2 + (y - 2)2 = (x + 1)2 + (y - 4)2
x2 - 2x + 1 + y2 - 4y + 4 = x2 + 2x + 1 + y2 - 8y + 16
-2x - 4y + 5 = 2x - 8y + 17
4x - 4y + 12 = 0
x - y + 3 = 0
y = x + 3
Vì M thuộc đồ thị hàm số y = 2x + 3 nên ta có:
x + 3 = 2x + 3
x = 0
y = 0 + 3 = 3
Vậy M(0; 3).
Để củng cố kiến thức về hàm số bậc nhất và ứng dụng vào giải bài tập, các em có thể luyện tập thêm các bài tập sau:
Bài 17 trang 112 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.