Bài 33 trang 91 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 33 trang 91 sách bài tập toán 9 - Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC có \(\widehat A = 70^\circ ,AB = 10cm,AC = 15cm\). Tính BC.
Đề bài
Cho tam giác ABC có \(\widehat A = 70^\circ ,AB = 10cm,AC = 15cm\). Tính BC.
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông ABH, từ đó tính được AH, BH.
Bước 2: Tính \(CH = AC - AH\).
Bước 3: Áp dụng định lý Pythagore trong tam giác BCH để tính BC.
Lời giải chi tiết
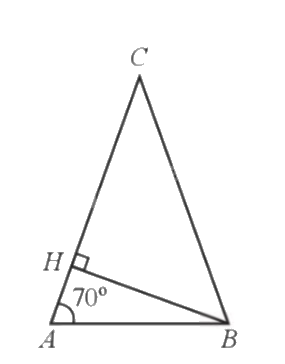
Kẻ đường cao BH của tam giác ABC.
Xét tam giác ABH vuông tại H ta có: \(\sin A = \frac{{HB}}{{AB}}\) nên \(BH = AB.\sin A = 10.\sin 70^\circ \).
Và \(\cos A = \frac{{HA}}{{AB}}\) nên \(AH = AB.\cos A = 10.\cos 70^\circ \).
Ta có \(AH = AB.\cos A = 10.\cos 70^\circ \)
Mặt khác, \(CH = AC - AH = 15 - 10.\cos 70^\circ .\)
Xét tam giác BCH vuông tại H, áp dụng định lý Pythagore, ta có
\(BC = \sqrt {B{H^2} + C{H^2}} \\= \sqrt {{{\left( {10.\sin 70^\circ } \right)}^2} + {{\left( {15 - 10.\cos 70^\circ } \right)}^2}} \approx 14,9\)m.
Bài 33 trang 91 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số góc, đường thẳng song song, vuông góc, và ứng dụng vào giải quyết các bài toán liên quan đến thực tế.
Bài 33 bao gồm các câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh khác nhau của hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:
Để xác định hệ số góc của đường thẳng, học sinh cần đưa phương trình về dạng y = ax + b. Sau đó, hệ số a chính là hệ số góc của đường thẳng.
Ví dụ: Nếu phương trình đường thẳng là 2x + 3y = 6, ta có thể viết lại thành y = (-2/3)x + 2. Vậy hệ số góc của đường thẳng là -2/3.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2.
Học sinh cần so sánh hệ số góc của hai đường thẳng. Nếu hai hệ số góc bằng nhau và hai đường thẳng không trùng nhau, thì hai đường thẳng song song.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 vuông góc khi và chỉ khi a1 * a2 = -1.
Học sinh cần nhân hệ số góc của hai đường thẳng. Nếu tích bằng -1, thì hai đường thẳng vuông góc.
Cho hai đường thẳng d1: y = 2x + 1 và d2: y = -1/2x + 3. Hãy xác định xem hai đường thẳng này có song song, vuông góc hay không?
Giải:
Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập toán 9 - Cánh diều tập 1. Ngoài ra, có rất nhiều tài liệu học tập trực tuyến và các bài giảng video trên Giaitoan.edu.vn có thể giúp các em hiểu rõ hơn về hàm số và các ứng dụng của nó.
Bài 33 trang 91 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về hàm số. Bằng cách nắm vững kiến thức cơ bản và luyện tập thường xuyên, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.