Bài 42 trang 121 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 42 trang 121 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
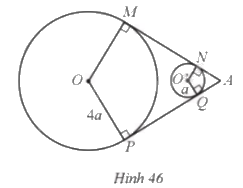
Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho \(\widehat {MAP} = 60^\circ \) (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.
Đề bài
Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho \(\widehat {MAP} = 60^\circ \) (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.
Phương pháp giải - Xem chi tiết
Độ dài dây curoa = độ dài cung lớn MP + độ dài cung nhỏ NQ + MN + PQ
Bước 1: Áp dụng lý thuyết về tổng 4 góc trong tứ giác để tính số đo góc MOP và góc NO’Q, từ đó suy ra số đo cung lớn MP và cung nhỏ NQ.
Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\) để tính độ dài 2 cung trên.
Bước 3: Chứng minh \(MN = PQ\), tính \(MN = AM - AN = OM.\cot \widehat {OAM} - O'N.\cot \widehat {OAM}\).
Lời giải chi tiết
Do AM, AP là tiếp tuyến của (O) nên \(MA = PA\) và \(OM \bot MA,OP \bot PA\), do đó \(\widehat M = \widehat P = 90^\circ \) và AO là tia phân giác của góc MAP nên \(\widehat {MAO} = \widehat {PAO} = \frac{{\widehat {MAP}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Do AN, AQ là tiếp tuyến của (O’) nên \(NA = QA\) và \(O'N \bot NA,O'Q \bot QA\), do đó \(\widehat {O'NA} = \widehat {O'QA} = 90^\circ \) và AO’ là tia phân giác của góc NAQ nên \(\widehat {NAO'} = \widehat {QAO'} = \frac{{\widehat {NAQ}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \)
Xét tứ giác OMAP có \(\widehat {MOP} + \widehat M + \widehat {MAP} + \widehat P = 360^\circ \) nên \(\widehat {MOP} = 360^\circ - \left( {\widehat M + \widehat {MAP} + \widehat P} \right)\)\( = 360^\circ - \left( {90^\circ + 60^\circ + 90^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ MP là 120⁰
Số đo cung lớn MP là \(360^\circ - 120^\circ = 240^\circ \) và có độ dài là \({l_1} = \frac{{\pi .4a.240}}{{180}} = \frac{{16\pi a}}{3}\)
Xét tứ giác O’NAQ có \(\widehat {NO'Q} + \widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ} = 360^\circ \) nên \(\widehat {NO'Q} = 360^\circ - \left( {\widehat {O'NA} + \widehat {O'QA} + \widehat {NAQ}} \right)\) \( = 360^\circ - \left( {90^\circ + 90^\circ + 60^\circ } \right) = 120^\circ \), suy ra số đo cung nhỏ NQ là 120⁰ và có độ dài là \({l_2} = \frac{{\pi .a.120}}{{180}} = \frac{{2\pi a}}{3}\)
Ta có: \(MN = MA - NA;PQ = PA - QA\), mà \(MA = PA;NA = QA\) suy ra \(MN = PQ\).
Xét tam giác OAM vuông tại M có:
\(MA = OM.\cot \widehat {OAM} = a.\cot 30^\circ = 4a\sqrt 3 \).
Xét tam giác O’AN vuông tại N có:
\(NA = ON.\cot O'AN = a.\cot 30^\circ = a\sqrt 3 \).
Ta có: \(MN = PQ = MA - NA = 4a\sqrt 3 - a\sqrt 3 = 3\sqrt 3 a\)
Độ dài dây Curoa mắc qua 2 ròng rọc là:
\(\frac{{16\pi a}}{3} + \frac{{2\pi a}}{3} + 3\sqrt 3 a + 3\sqrt 3 a = 6a\left( {\pi + \sqrt 3 } \right)\).
Bài 42 trang 121 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số a, b, c của hàm số, tìm đỉnh của parabol, vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 42 trang 121 sách bài tập Toán 9 Cánh diều tập 1, chúng ta cần phân tích kỹ đề bài và áp dụng các kiến thức đã học. Dưới đây là hướng dẫn chi tiết cho từng câu hỏi:
Ví dụ: Cho hàm số y = 2x2 - 5x + 3. Xác định hệ số a, b, c.
Giải: Ta có a = 2, b = -5, c = 3.
Ví dụ: Cho hàm số y = x2 - 4x + 1. Tìm đỉnh của parabol.
Giải: Ta có a = 1, b = -4, c = 1. Khi đó, x0 = -(-4)/(2*1) = 2 và y0 = -( (-4)2 - 4*1*1 )/(4*1) = -12/4 = -3. Vậy đỉnh của parabol là I(2; -3).
Để vẽ đồ thị hàm số, ta cần xác định đỉnh, trục đối xứng và một vài điểm thuộc đồ thị. Sau đó, nối các điểm lại với nhau để được parabol.
Các bài toán ứng dụng thường yêu cầu học sinh thiết lập hàm số dựa trên các thông tin đề bài cung cấp, sau đó tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 1 và các đề thi thử Toán 9.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 42 trang 121 sách bài tập Toán 9 Cánh diều tập 1 và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học.