Bài 24 trang 109 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 24 trang 109 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
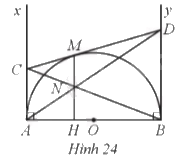
Cho nửa đường tròn tâm O đường kính AB, kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyển thứ ba cắt Ax, By lần lượt tại C, D. Gọi N là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24).
Đề bài
Cho nửa đường tròn tâm O đường kính AB, kẻ các tiếp tuyến Ax, By của đường tròn (O). Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyển thứ ba cắt Ax, By lần lượt tại C, D. Gọi N là giao điểm của AD và BC và H là giao điểm của MN và AB (Hình 24).
Chứng minh:
a) \(MN \bot AB\)
b) \(MN = NH\)
Phương pháp giải - Xem chi tiết
a) Bước 1: Chứng minh \(AC = CM,BD = DM\)
Bước 2: Áp dụng định lý Thales trong các tam giác ANC, ACD để suy ra \(\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}\)
b) Áp dụng định lý Thales trong các tam giác CAD, CAN, CBA suy ra \(\frac{{MN}}{{AC}} = \frac{{NH}}{{CA}}\)
Lời giải chi tiết
a) Ta có \(Ax \bot AB,By \bot AB\) (do Ax, By là tiếp tuyến của (O)) nên \(Ax//By\).
Mặt khác, do Ax, By, CD là tiếp tuyến của (O)) nên \(AC = CM,BD = DM\).
Xét tam giác ANC có \(AC//BD\), áp dụng định lý Thales ta được \(\frac{{NA}}{{ND}} = \frac{{AC}}{{BD}}\)
nên \(\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}\).
Xét tam giác CAD có \(\frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}\)\(\left( {N \in AD,M \in CD} \right)\) do đó \(MN//AC\).
Mà \(AC \bot AB\) suy ra \(MN \bot AB\).
b) Áp dụng định lý Thales trong:
Tam giác CAD có \(MN//AC\): \(\frac{{MN}}{{AC}} = \frac{{DN}}{{AD}}\)(1)
Tam giác CAN có \(CA//BD\): \(\frac{{DN}}{{AD}} = \frac{{BN}}{{CB}}\) (2)
Tam giác CBA có \(NH//CA\): \(\frac{{BN}}{{CB}} = \frac{{NH}}{{CA}}\) (3)
Từ (1), (2), (3) suy ra \(\frac{{MN}}{{AC}} = \frac{{NH}}{{CA}}\), do đó \(MN = NH\)
Bài 24 trang 109 sách bài tập Toán 9 - Cánh diều tập 1 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số trong thực tế.
Bài 24 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 24 trang 109 sách bài tập Toán 9 - Cánh diều tập 1, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập.
Đề bài: Cho hàm số y = 2x - 3. Hãy xác định hệ số a, b và vẽ đồ thị hàm số.
Lời giải:
Để giải bài tập về hàm số bậc nhất và hàm số bậc hai một cách hiệu quả, các em học sinh cần:
Các em học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Bài 24 trang 109 sách bài tập Toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.