Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 14 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Đề bài
Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Phương pháp giải - Xem chi tiết
Chứng minh ngược lại: Giả sử có hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường. Sau đó chứng minh giả sử là sai.
Lời giải chi tiết
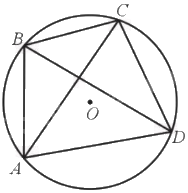
Giả sử trái lại có hai dây cung BD và AC (không đi qua tâm O) cắt nhau tại trung điểm mỗi đường.
Suy ra tứ giác ABCD là hình bình hành.
Do đó \(\widehat {ABC} = \widehat {ADC}\).
Mặt khác, tứ giác ABCD nội tiếp nên \(\widehat {ABC} + \widehat {ADC} = {180^o}\).
Suy ra \(\widehat {ABC} = \widehat {ADC} = {90^o}\), từ đó suy ra AC là đường kính của đường tròn (O) hay AC đi qua tâm O, mâu thuẫn với điều giả sử.
Vậy trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Bài 14 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số, và cách xác định phương trình đường thẳng.
Bài 14 bao gồm các dạng bài tập sau:
Để xác định hệ số góc của đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Nếu a > 0, đường thẳng đồng biến; nếu a < 0, đường thẳng nghịch biến; nếu a = 0, đường thẳng là đường thẳng ngang.
Ví dụ: Xác định hệ số góc của đường thẳng y = 2x - 3.
Giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Để tìm giao điểm của hai đường thẳng y = a1x + b1 và y = a2x + b2, ta giải hệ phương trình:
{ y = a1x + b1 y = a2x + b2 }
Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải: Giải hệ phương trình:
{ y = x + 1 y = -x + 3 }
Ta có x + 1 = -x + 3 => 2x = 2 => x = 1. Thay x = 1 vào y = x + 1, ta được y = 2. Vậy giao điểm của hai đường thẳng là (1; 2).
Có nhiều cách để lập phương trình đường thẳng, tùy thuộc vào các yếu tố đã biết. Một số trường hợp thường gặp:
Các bài toán thực tế thường yêu cầu học sinh phải xây dựng mô hình toán học dựa trên các thông tin đã cho, sau đó sử dụng hàm số bậc nhất để giải quyết bài toán.
Bài 14 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt nhất.