Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 8 trang 10 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy logic và vận dụng kiến thức đã học. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
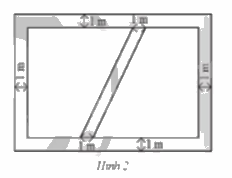
Một mảnh vườn có dạng hình chữ nhật với chiều rộng là 10 m. Chủ vườn đã làm con đường thảm cỏ (phần tô màu xám) với các kích thước như Hình 2. a) Tính chiều dài của mảnh vườn, biết tỉ số giữa diện tích của con đường thảm cỏ và diện tích của mảnh vườn là \(\frac{1}{3}.\) b) Biết rằng chi phí để hoàn thành mỗi mét vuông của con đường thảm cỏ là 100 000 đồng. Tính số tiền mà chủ vườn đã chi để làm con đường thảm cỏ đó.
Đề bài
Một mảnh vườn có dạng hình chữ nhật với chiều rộng là 10 m. Chủ vườn đã làm con đường thảm cỏ (phần tô màu xám) với các kích thước như Hình 2.
a) Tính chiều dài của mảnh vườn, biết tỉ số giữa diện tích của con đường thảm cỏ và diện tích của mảnh vườn là \(\frac{1}{3}.\)
b) Biết rằng chi phí để hoàn thành mỗi mét vuông của con đường thảm cỏ là 100 000 đồng. Tính số tiền mà chủ vườn đã chi để làm con đường thảm cỏ đó.
Phương pháp giải - Xem chi tiết
a) Bước 1: Gọi chiều dài của mảnh vườn là \(x(m),x > 10.\)
Bước 2: Biểu diễn diện tích mảnh vườn, diện tích thảm cỏ qua biến \(x\) và dữ kiện đã cho.
Bước 3: Lập phương trình: tỉ số giữa diện tích của con đường thảm cỏ và diện tích của mảnh vườn là \(\frac{1}{3}.\)
b) Số tiền đã chi = diện tích thảm cỏ x 100 000 đồng.
Lời giải chi tiết
a) Gọi chiều dài của mảnh vườn là \(x(m),x > 10.\)
Diện tích mảnh vườn là \(10x({m^2}).\)
Diện tích của con đường thảm cỏ là:
\(2.10.1 + 2.(x - 2).1 + 1.(10 - 2) = 2x + 24({m^2}).\)
Do diện tích của con đường thảm cỏ và diện tích của mảnh vườn là \(\frac{1}{3}\) nên ta có phương trình:
\(\begin{array}{l}\frac{{2x + 24}}{{10x}} = \frac{1}{3}\\3\left( {2x + 24} \right) = 10x\\4x = 72\\x = 18(tm)\end{array}\)
Vậy chiều dài mảnh vườn là 18 mét.
b) Diện tích con đường thảm cỏ là:
\(2x + 24 = 2.18 + 24 = 60({m^2}).\)
Số tiền mà chủ vườn đã chi để làm con đường thảm cỏ là:
\(60.100\,000 = 6\,000\,000\) đồng.
Bài 8 trang 10 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình đại số, tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi biểu thức đại số. Bài tập này yêu cầu học sinh vận dụng các quy tắc, công thức đã học để rút gọn biểu thức, tìm giá trị của biểu thức, hoặc chứng minh đẳng thức.
Bài 8 bao gồm một số câu hỏi nhỏ, mỗi câu hỏi yêu cầu thực hiện một phép biến đổi hoặc tính toán cụ thể. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Để rút gọn biểu thức, bạn cần thực hiện các phép toán theo đúng thứ tự ưu tiên (ngoặc trước, nhân chia trước, cộng trừ sau). Sử dụng các hằng đẳng thức đại số để biến đổi biểu thức về dạng đơn giản nhất.
Ví dụ: Nếu biểu thức là (x + y)^2 - (x - y)^2, bạn có thể sử dụng hằng đẳng thức (a + b)^2 = a^2 + 2ab + b^2 và (a - b)^2 = a^2 - 2ab + b^2 để rút gọn biểu thức thành 4xy.
Để tìm giá trị của biểu thức, bạn cần thay giá trị của các biến vào biểu thức và thực hiện các phép tính. Lưu ý kiểm tra xem các giá trị của biến có thỏa mãn điều kiện của biểu thức hay không.
Ví dụ: Nếu biểu thức là x^2 + 2x + 1 và x = -1, bạn thay x = -1 vào biểu thức và tính được giá trị là 0.
Để chứng minh đẳng thức, bạn cần biến đổi một vế của đẳng thức về dạng tương đương với vế còn lại. Sử dụng các phép biến đổi đại số và các hằng đẳng thức để thực hiện việc chứng minh.
Ví dụ: Để chứng minh (x + y)^2 = x^2 + 2xy + y^2, bạn có thể khai triển vế trái (x + y)^2 thành x^2 + 2xy + y^2, và thấy rằng nó bằng vế phải.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập toán 9 - Cánh diều tập 1, hoặc tìm kiếm trên các trang web học toán online.
Bài 8 trang 10 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp bạn ôn tập và củng cố kiến thức về các phép biến đổi biểu thức đại số. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!