Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 15 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải chi tiết dưới đây!
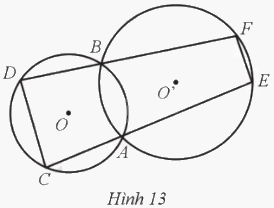
Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD.
Đề bài
Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD.
Phương pháp giải - Xem chi tiết
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng 180o.
Lời giải chi tiết
Ta có tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {ACD} = \widehat {ABF}( = {180^o} - \widehat {ABD})\) (1).
Mặt khác, tứ giác ABFE nội tiếp đường tròn (O’) suy ra \(\widehat {ABF} + \widehat {AEF} = {180^o}\) (2).
Từ (1) và (2) ta có \(\widehat {ACD} + \widehat {AEF} = {180^o}\) hay \(\widehat {ECD} + \widehat {CEF} = {180^o}\). Suy ra EF // CD.
Bài 15 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 15 bao gồm các dạng bài tập sau:
Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Giải:
Hàm số y = 2x - 3 có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
So sánh với dạng tổng quát, ta có a = 2 và b = -3.
Vậy, hệ số góc của hàm số là 2 và tung độ gốc là -3.
Tìm tọa độ giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải:
Để tìm tọa độ giao điểm của hai đường thẳng, ta giải hệ phương trình:
{ y = x + 1 y = -x + 3 }
Thay y = x + 1 vào phương trình y = -x + 3, ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 1, ta được:
y = 1 + 1 = 2
Vậy, tọa độ giao điểm của hai đường thẳng là (1; 2).
Một người đi xe máy từ A đến B với vận tốc 40 km/h. Sau 1 giờ 30 phút, người đó còn cách B 50 km. Tính độ dài quãng đường AB.
Giải:
Thời gian người đó đi được là 1 giờ 30 phút = 1,5 giờ.
Quãng đường người đó đi được là 40 km/h * 1,5 giờ = 60 km.
Độ dài quãng đường AB là 60 km + 50 km = 110 km.
Bài 15 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!