Giải bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2

Bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ với các kích thước như ở Hình 24. Hỏi thể tích của bồn chứa bằng bao nhiêu mét khối (làm tròn kết quả đến hàng phần mười)?

Đề bài

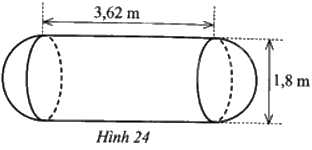
Giải bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 1

Phương pháp giải - Xem chi tiết Giải bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 2

Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).

Thể tích của hình trụ: \(V = \pi {R^2}h\).

Lời giải chi tiết

Ta có bán kính hình cầu và bán kính đáy hình trụ đều là: 1,8 : 2 = 0,9 (m).

Tổng thể tích của hai nửa hình cầu chính là thể tích của một hình cầu có cùng bán kính và bằng: \(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{(0,9)^3} = 0,972\pi \) (m³).

Thể tích phần hình trụ là:

V = πR²h = π.(0,9)².3,62 = 2,9322π (m³).

Thể tích của bồn chứa là:

0,972π + 2,9322π = 3,9042π ≈ 3,9042.3,14 ≈ 12,3 (m³).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 đặc sắc thuộc chuyên mục giải bài tập toán 9 trên nền tảng môn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2: Hướng dẫn chi tiết

Bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, giaitoan.edu.vn xin trình bày chi tiết lời giải và các bước thực hiện.

Phân tích đề bài

Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 27 thường yêu cầu học sinh:

Xác định hàm số bậc nhất hoặc bậc hai dựa trên các thông tin đề bài cung cấp.
Tìm các hệ số của hàm số.
Giải các phương trình hoặc bất phương trình liên quan đến hàm số.
Vận dụng hàm số để giải quyết các bài toán thực tế, ví dụ như tính quãng đường, thời gian, hoặc chi phí.

Lời giải chi tiết bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2

(Nội dung lời giải chi tiết bài 27 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ, nếu bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm, lời giải sẽ hướng dẫn cách sử dụng công thức tính hệ số góc và hệ số tự do, sau đó viết phương trình đường thẳng.)

Ví dụ minh họa

Để giúp học sinh hiểu rõ hơn về cách giải bài tập, chúng ta sẽ xem xét một ví dụ minh họa:

Ví dụ: Cho hai điểm A(1; 2) và B(3; 4). Hãy tìm phương trình đường thẳng đi qua hai điểm này.

Tính hệ số góc: m = (y₂ - y₁) / (x₂ - x₁) = (4 - 2) / (3 - 1) = 1
Sử dụng công thức phương trình đường thẳng: y - y₁ = m(x - x₁)
Thay các giá trị vào: y - 2 = 1(x - 1)
Rút gọn phương trình: y = x + 1

Vậy phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4) là y = x + 1.

Lưu ý khi giải bài tập

Khi giải bài tập về hàm số bậc nhất và hàm số bậc hai, học sinh cần lưu ý những điều sau:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Vận dụng đúng các công thức và định lý đã học.
Kiểm tra lại kết quả sau khi giải xong.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Ứng dụng của hàm số trong thực tế

Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như:

Tính toán chi phí sản xuất.
Dự báo doanh thu.
Mô tả sự thay đổi của các đại lượng vật lý.
Giải quyết các bài toán tối ưu hóa.

Tổng kết

Bài 27 trang 135 sách bài tập toán 9 - Cánh diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và tự tin làm bài tập.

Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn toán. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải toán 9 khác và các tài liệu học tập hữu ích.