Giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết và kèm theo các giải thích cụ thể để giúp bạn hiểu rõ bản chất của bài toán.

Một chiếc đèn khung tre đan trang trí phòng khách có dạng hai hình trụ với cùng chiều cao được lồng vào nhau (Hình 6a). Mặt xung quanh của hình trụ bên trong được dán bằng vải màu mỡ gà, mặt xung quanh của hình trụ bên ngoài được dán bằng vải màu tím. Các kích thước của hai hình trụ đó được mô tả như ở Hình 6b. a) Tính tỉ số phần trăm diện tích vải màu mỡ gà và diện tích vải màu tím cần sử dụng. b) Hỏi tổng số tiền mua vải màu tím và vải màu mỡ gà để làm chiếc đèn đó bằng bao nhiêu nghìn đồng

Đề bài

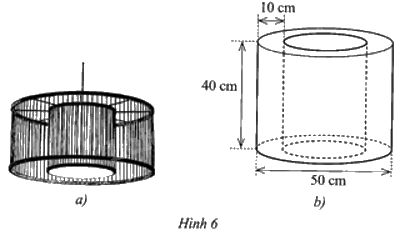
Giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 1

a) Tính tỉ số phần trăm diện tích vải màu mỡ gà và diện tích vải màu tím cần sử dụng.

b) Hỏi tổng số tiền mua vải màu tím và vải màu mỡ gà để làm chiếc đèn đó bằng bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)? Biết 1 m² vải màu tím và 1 m² vải màu mỡ gà có giá lần lượt là 95 nghìn đồng và 115 nghìn đồng.

Phương pháp giải - Xem chi tiết Giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 2

Dựa vào: Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rh\)

Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right)\)

Lời giải chi tiết

a) Bán kính đáy của hình trụ bên ngoài là: 50 : 2 = 25 (cm).

Diện tích vải màu tím cần dùng là: 2π.25.40 = 2 000π (cm²).

Bán kính đáy của hình trụ bên trong là: \(\frac{{50 - 10 - 10}}{2} = 15\) (cm).

Diện tích vải màu mỡ gà cần dùng là: 2π.15.40 = 1 200π (cm²).

Tỉ số phần trăm diện tích vải màu mỡ gà và diện tích vải màu tím cần dùng là

\(\frac{{1200\pi .100}}{{2000\pi }}\% = 60\% \).

b) Đổi 2 000π cm² = 0,2π m²; 1 200π cm² = 0,12π m².

Số tiền mua vải màu tím là:

0,2π . 95 = 19π (nghìn đồng).

Số tiền mua vải màu mỡ gà là:

0,12π . 115 = 13,8π (nghìn đồng).

Tổng số tiền mua vải màu tím và vải màu mỡ gà để làm được chiếc đèn đó là:

19π + 13,8π = 32,8π ≈ 32,8.3,14 = 102,992 ≈ 103 (nghìn đồng).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 đặc sắc thuộc chuyên mục toán lớp 9 trên nền tảng đề thi toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2: Tổng quan

Bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và tìm các điểm đặc biệt của đồ thị.

Nội dung bài tập

Bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 thường bao gồm các dạng bài tập sau:

Dạng 1: Xác định hàm số bậc nhất. Học sinh cần xác định các hệ số a, b trong hàm số y = ax + b dựa vào các thông tin cho trước.
Dạng 2: Vẽ đồ thị hàm số bậc nhất. Học sinh cần vẽ đồ thị của hàm số y = ax + b dựa vào các điểm thuộc đồ thị hoặc các thông tin về hệ số a, b.
Dạng 3: Tìm giao điểm của hai đường thẳng. Học sinh cần tìm tọa độ giao điểm của hai đường thẳng bằng phương pháp giải hệ phương trình.
Dạng 4: Ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế. Học sinh cần vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến các tình huống thực tế.

Hướng dẫn giải chi tiết bài 6 trang 125

Để giúp bạn giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2 một cách hiệu quả, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng dạng bài tập:

Dạng 1: Xác định hàm số bậc nhất

Để xác định hàm số bậc nhất y = ax + b, bạn cần tìm các hệ số a và b. Thông thường, đề bài sẽ cung cấp các thông tin như:

Hai điểm thuộc đồ thị hàm số.
Hệ số góc a và tung độ gốc b.
Các thông tin liên quan đến độ dốc và vị trí của đường thẳng.

Sau khi có đủ thông tin, bạn có thể sử dụng các công thức và phương pháp đại số để tìm ra giá trị của a và b, từ đó xác định được hàm số bậc nhất.

Dạng 2: Vẽ đồ thị hàm số bậc nhất

Để vẽ đồ thị hàm số y = ax + b, bạn cần xác định ít nhất hai điểm thuộc đồ thị. Bạn có thể chọn các điểm có hoành độ hoặc tung độ dễ tính toán. Sau khi có hai điểm, bạn nối chúng lại bằng một đường thẳng để được đồ thị của hàm số.

Lưu ý rằng, nếu a > 0 thì hàm số đồng biến, đồ thị là một đường thẳng đi lên từ trái sang phải. Nếu a < 0 thì hàm số nghịch biến, đồ thị là một đường thẳng đi xuống từ trái sang phải.

Dạng 3: Tìm giao điểm của hai đường thẳng

Để tìm giao điểm của hai đường thẳng y = a1x + b1 và y = a2x + b2, bạn cần giải hệ phương trình sau:

{ y = a1x + b1

y = a2x + b2 }

Có nhiều phương pháp để giải hệ phương trình này, như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp đồ thị. Sau khi giải được hệ phương trình, bạn sẽ tìm được tọa độ giao điểm (x0, y0) của hai đường thẳng.

Dạng 4: Ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế

Khi giải các bài toán thực tế liên quan đến hàm số bậc nhất, bạn cần:

Xác định các đại lượng liên quan và mối quan hệ giữa chúng.
Biểu diễn mối quan hệ này bằng một hàm số bậc nhất.
Sử dụng hàm số bậc nhất để giải quyết bài toán.

Ví dụ minh họa

Ví dụ: Cho hàm số y = 2x - 1. Hãy xác định hàm số và vẽ đồ thị của nó.

Giải:

Hàm số y = 2x - 1 là một hàm số bậc nhất với hệ số a = 2 và b = -1.

Để vẽ đồ thị của hàm số, ta xác định hai điểm thuộc đồ thị:

Khi x = 0, y = 2(0) - 1 = -1. Vậy điểm A(0, -1) thuộc đồ thị.
Khi x = 1, y = 2(1) - 1 = 1. Vậy điểm B(1, 1) thuộc đồ thị.

Nối hai điểm A và B lại bằng một đường thẳng, ta được đồ thị của hàm số y = 2x - 1.

Lời khuyên

Để học tốt môn toán 9, bạn cần:

Nắm vững các kiến thức cơ bản về hàm số bậc nhất.
Luyện tập thường xuyên các bài tập khác nhau.
Tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.
Sử dụng các tài liệu học tập và công cụ hỗ trợ trực tuyến.

Giaitoan.edu.vn hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 6 trang 125 sách bài tập toán 9 - Cánh diều tập 2. Chúc bạn học tập tốt!