Bài 12 trang 106 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 106 SBT Toán 9 Cánh diều tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho \(\widehat {xOy} = 30^\circ \) và điểm O’ thuộc tia Oy sao cho OO’ = 4 cm. a) Tính khoảng cách từ điểm O’ đến tia Oy, b) Xác định vị trí tương đối của tia Oy và đường tròn (O’; R) tuỳ theo độ dài R với \(R \le 4\) cm.
Đề bài
Cho \(\widehat {xOy} = 30^\circ \) và điểm O’ thuộc tia Oy sao cho OO’ = 4 cm.
a) Tính khoảng cách từ điểm O’ đến tia Oy,
b) Xác định vị trí tương đối của tia Oy và đường tròn (O’; R) tuỳ theo độ dài R với
\(R \le 4\) cm.
Phương pháp giải - Xem chi tiết
a) Áp dụng tỉ số lượng giác trong tam giác vuông OO’H để tính O’H.
b) Biện luận các trường hợp theo khoảng cách O’H và R.
Lời giải chi tiết
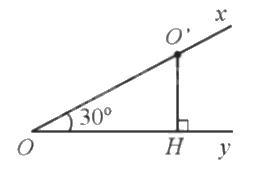
a) Kẻ \(O'H \bot Oy\) \(\left( {H \in Oy} \right)\).
Xét tam giác O’OH vuông tại H, ta có \(\sin O = \frac{{O'H}}{{OO'}}\) hay \(O'H = OO'.\sin O = 4\sin 30^\circ = 2\)cm.
Vậy khoảng cách từ điểm O’ đến tia Oy là 2cm.
b) Vì khoảng cách từ O’ đến Oy là 2cm nên:
Nếu \(R < 2\)cm: Oy và (O’) không cắt nhau
Nếu \(R = 2\)cm: Oy và (O’) tiếp xúc nhau
Nếu \(2 < R < 4\): Oy và (O’) cắt nhau
Bài 12 trang 106 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đường thẳng, hệ số góc, và mối quan hệ giữa các đường thẳng.
Bài 12 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 12 trang 106, chúng ta sẽ đi vào phân tích từng phần của bài tập.
Để xác định hệ số góc của một đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Hệ số a được gọi là hệ số góc của đường thẳng.
Ví dụ: Đường thẳng y = 2x + 3 có hệ số góc là 2.
Để viết phương trình đường thẳng khi biết hệ số góc a và một điểm thuộc đường thẳng (x0, y0), ta sử dụng công thức:
y - y0 = a(x - x0)
Ví dụ: Viết phương trình đường thẳng có hệ số góc là -1 và đi qua điểm (1, 2).
Áp dụng công thức, ta có: y - 2 = -1(x - 1) => y - 2 = -x + 1 => y = -x + 3
Hai đường thẳng y = a1x + b1 và y = a2x + b2:
Các bài toán thực tế thường yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để mô tả mối quan hệ giữa các đại lượng và giải quyết các vấn đề liên quan.
Ví dụ: Một người đi xe đạp với vận tốc không đổi là 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian.
Gọi x là thời gian (giờ) và y là quãng đường đi được (km). Ta có hàm số: y = 15x
Bài 12 trang 106 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.