Bài 23 trang 21 sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 23 trang 21 sách bài tập Toán 9 - Cánh Diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
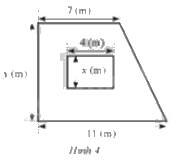
Một cửa số có dạng hình chữ nhật được xây trên bức tường có dạng hình thang vuông với các kích thước như Hình 4. Tìm x, y, biết rằng diện tích của bức tưởng không tính phần làm cửa sổ là 69 m2 và 2x = y - 3.
Đề bài
Một cửa số có dạng hình chữ nhật được xây trên bức tường có dạng hình thang vuông với các kích thước như Hình 4. Tìm x, y, biết rằng diện tích của bức tưởng không tính phần làm cửa sổ là 69 m2 và 2x = y - 3.
Phương pháp giải - Xem chi tiết
Bước 1: Tính diện tích bức tường hình thang vuông.
Bước 2: Tính diện tích cửa sổ.
Bước 3: Diện tích bức tường không có cửa sổ = diện tích hình thang vuông – diện tích cửa sổ (lập phương trình).
Bước 4: Rút y từ phương trình đã cho, thế vào phương trình vừa lập được.
Bước 5: Giải phương trình và đối chiếu điều kiện.
Lời giải chi tiết
Diện tích bức tường hình thang vuông là: \(\frac{{\left( {7 + 11} \right)y}}{2}\left( {{m^2}} \right).\)
Diện tích cửa sổ là: \(4x\left( {{m^2}} \right).\)
Do diện tích phần còn lại là 69m2 nên ta có phương trình \(\frac{{\left( {7 + 11} \right)y}}{2} - 4x = 69\) hay \(9y - 4x = 69\) (1).
Từ phương trình \(2x = y - 3\) ta có \(y = 2x + 3\) (2).
Thế (2) vào (1) ta được \(9\left( {2x + 3} \right) - 4x = 69\)
Giải phương trình trên:
\(\begin{array}{l}18x + 27 - 4x = 69\\14x = 42\\x = 3\end{array}\)
Thay \(x = 3\) vào phương trình (2) ta được \(y = 2.3 + 3 = 9\).
Vậy \(x = 3,y = 9\) là các giá trị cần tìm.
Bài 23 trang 21 sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Phương pháp giải bài tập thường bao gồm các bước sau:
Bài 23: Cho hàm số y = 2x + 3.
(a) Vẽ đồ thị của hàm số.
Để vẽ đồ thị của hàm số y = 2x + 3, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = 2(0) + 3 = 3. Vậy điểm A(0; 3) thuộc đồ thị. Chọn x = 1, ta có y = 2(1) + 3 = 5. Vậy điểm B(1; 5) thuộc đồ thị.
Vẽ đường thẳng đi qua hai điểm A(0; 3) và B(1; 5), ta được đồ thị của hàm số y = 2x + 3.
(b) Tìm tọa độ giao điểm của đồ thị hàm số với đường thẳng y = -x + 6.
Để tìm tọa độ giao điểm của hai đường thẳng y = 2x + 3 và y = -x + 6, ta giải hệ phương trình:
{ y = 2x + 3 y = -x + 6 }
Thay y = 2x + 3 vào phương trình y = -x + 6, ta được:
2x + 3 = -x + 6
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 3, ta được:
y = 2(1) + 3 = 5
Vậy tọa độ giao điểm của hai đường thẳng là (1; 5).
(c) Tìm các điểm M(x; y) thuộc đồ thị hàm số sao cho x + y = 8.
Để tìm các điểm M(x; y) thuộc đồ thị hàm số y = 2x + 3 sao cho x + y = 8, ta thay y = 2x + 3 vào phương trình x + y = 8, ta được:
x + (2x + 3) = 8
3x + 3 = 8
3x = 5
x = 5/3
Thay x = 5/3 vào phương trình y = 2x + 3, ta được:
y = 2(5/3) + 3 = 10/3 + 9/3 = 19/3
Vậy điểm M(5/3; 19/3) thuộc đồ thị hàm số y = 2x + 3 và thỏa mãn x + y = 8.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể luyện tập thêm các bài tập sau:
Bài 23 trang 21 sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.