Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy logic và vận dụng kiến thức đã học. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, chi tiết, kèm theo các bước giải cụ thể để bạn có thể dễ dàng theo dõi và nắm bắt.

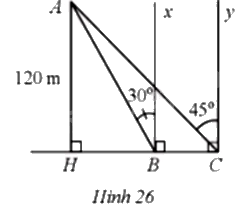
Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là \(\widehat {ABx} = 30^\circ ,\widehat {ACx} = 45^\circ \) (hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).

Đề bài

Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 2

Bước 1: Áp dụng tỉ số lượng giác trong các tam giác vuông AHB và AHC để tính HB, HC.

Bước 2: \(BC = HC - HB\).

Lời giải chi tiết

Ta có \(AH \bot HC,Bx \bot HC,Cy \bot HC\) nên \(AH//Bx//Cy\).

Suy ra \(\widehat {ABx} = \widehat {HAB} = 30^\circ ,\widehat {ACx} = \widehat {CAH} = 45^\circ \) (các cặp góc so le trong).

Xét tam giác ABH vuông tại H, ta có \(\tan \widehat {HAB} = \frac{{BH}}{{AH}}\) hay \(BH = AH.\tan \widehat {HAB} = 120.\tan 30^\circ = 40\sqrt 3 \)m.

Xét tam giác ACH vuông tại H, ta có \(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(BH = CH.\tan \widehat {HAC} = 120.\tan 45^\circ = 120\)m.

Ta lại có \(BC = HC - HB = 120 - 40\sqrt 3 \approx 50,72\)m.

Vậy chiều dài của cây cầu khoảng 50,72m.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 đặc sắc thuộc chuyên mục bài tập toán 9 trên nền tảng học toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1: Tổng quan

Bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và tìm các điểm đặc biệt của đồ thị.

Nội dung bài tập

Bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 thường bao gồm các dạng bài tập sau:

Dạng 1: Xác định hàm số bậc nhất. Học sinh cần xác định các hệ số a, b trong hàm số y = ax + b dựa vào các thông tin cho trước.
Dạng 2: Vẽ đồ thị hàm số bậc nhất. Học sinh cần vẽ đồ thị của hàm số y = ax + b dựa vào các điểm thuộc đồ thị hoặc các thông tin về hệ số a, b.
Dạng 3: Tìm giao điểm của hai đường thẳng. Học sinh cần tìm tọa độ giao điểm của hai đường thẳng bằng phương pháp giải hệ phương trình.
Dạng 4: Ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế. Học sinh cần vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến các tình huống thực tế.

Hướng dẫn giải chi tiết bài 26 trang 89

Để giúp bạn giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 một cách dễ dàng, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng dạng bài tập:

Dạng 1: Xác định hàm số bậc nhất

Để xác định hàm số bậc nhất y = ax + b, bạn cần tìm các hệ số a và b. Thông thường, đề bài sẽ cung cấp các thông tin như:

Hai điểm thuộc đồ thị hàm số.
Hệ số góc a và tung độ gốc b.
Các thông tin khác liên quan đến hàm số.

Sau khi có đủ thông tin, bạn có thể sử dụng các công thức và phương pháp đại số để tìm ra giá trị của a và b.

Dạng 2: Vẽ đồ thị hàm số bậc nhất

Để vẽ đồ thị hàm số y = ax + b, bạn cần xác định ít nhất hai điểm thuộc đồ thị. Bạn có thể chọn hai giá trị tùy ý của x và tính giá trị tương ứng của y. Sau đó, vẽ hai điểm này lên hệ trục tọa độ và nối chúng lại bằng một đường thẳng. Đường thẳng này chính là đồ thị của hàm số.

Dạng 3: Tìm giao điểm của hai đường thẳng

Để tìm giao điểm của hai đường thẳng y = a1x + b1 và y = a2x + b2, bạn cần giải hệ phương trình sau:

{ y = a1x + b1

y = a2x + b2

Có nhiều phương pháp để giải hệ phương trình này, như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp đồ thị.

Dạng 4: Ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế

Khi giải các bài toán thực tế liên quan đến hàm số bậc nhất, bạn cần:

Đọc kỹ đề bài và xác định các yếu tố liên quan đến hàm số.
Xây dựng hàm số biểu diễn mối quan hệ giữa các yếu tố đó.
Giải phương trình hoặc hệ phương trình để tìm ra giá trị cần tìm.
Kiểm tra lại kết quả và đảm bảo rằng nó phù hợp với thực tế.

Ví dụ minh họa

Ví dụ 1: Xác định hàm số bậc nhất y = ax + b biết đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).

Giải: Thay tọa độ của hai điểm A và B vào phương trình y = ax + b, ta được hệ phương trình:

{ 2 = a + b

0 = -a + b

Giải hệ phương trình này, ta được a = 1 và b = 1. Vậy hàm số cần tìm là y = x + 1.

Lưu ý khi giải bài tập

Luôn kiểm tra lại kết quả sau khi giải xong.
Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
Tham khảo các tài liệu học tập và bài giảng của giáo viên.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Kết luận

Bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!