Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 39 trang 39 Sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
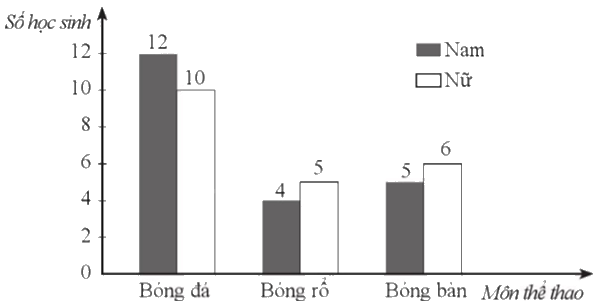
Thầy Nam điều tra sở thích chơi thể thao của học sinh lớp 9A do thầy phụ trách (mỗi học sinh chỉ nêu một môn thể thao yêu thích nhất). Biểu đồ cột kép ở Hình 20 biểu diễn số học sinh nam và số học sinh nữ của lớp 9A có sở thích chơi một số môn thể thao: Bóng đá, Bóng rổ, Bóng bàn mà thầy Nam đã điều tra. Chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra. Tính xác suất của mỗi biến cố sau: a) A: “Học sinh được chọn là nam"; b) B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá"; c)
Đề bài
Thầy Nam điều tra sở thích chơi thể thao của học sinh lớp 9A do thầy phụ trách (mỗi học sinh chỉ nêu một môn thể thao yêu thích nhất). Biểu đồ cột kép ở Hình 20 biểu diễn số học sinh nam và số học sinh nữ của lớp 9A có sở thích chơi một số môn thể thao: Bóng đá, Bóng rổ, Bóng bàn mà thầy Nam đã điều tra. Chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra. Tính xác suất của mỗi biến cố sau:
a) A: “Học sinh được chọn là nam";
b) B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá";
c) C: “Học sinh được chọn là nam và yêu thích môn Bóng bàn hoặc Bóng rổ".
Phương pháp giải - Xem chi tiết
Bước 1: Tính tổng số kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra.
Bước 2: Đếm số kết quả thuận lợi cho từng biến cố.
Bước 3: Lập tỉ số giữa số liệu ở bước 2 và bước 1.
Lời giải chi tiết
Các kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh của lớp 9A tham gia điều tra là: 12 +10 + 4 + 5 + 5 + 6 = 42 kết quả.
a) Các kết quả thuận lợi cho biến cố A: “Học sinh được chọn là nam" là: 12+ 4+ 5 = 21
Vậy \(P\left( A \right) = \frac{{21}}{{42}} = \frac{1}{2}\)
b) Các kết quả thuận lợi cho biến cố B: “Học sinh được chọn là nữ và yêu thích môn Bóng đá" là 10.
Vậy \(P\left( B \right) = \frac{{10}}{{42}} = \frac{5}{{21}}\).
c) Các kết quả thuận lợi cho biến cố C: “Học sinh được chọn là nam và yêu thích môn Bóng bàn hoặc Bóng rổ" là:4 + 5 = 9.
Vậy \(P\left( C \right) = \frac{9}{{42}} = \frac{3}{{14}}.\).
Bài 39 trang 39 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, biểu đồ hàm số và ứng dụng của hàm số trong đời sống.
Bài 39 trang 39 Sách bài tập Toán 9 - Cánh Diều tập 2 thường bao gồm các dạng bài tập sau:
Để giúp bạn giải bài 39 trang 39 Sách bài tập Toán 9 - Cánh Diều tập 2 một cách dễ dàng, chúng tôi sẽ cung cấp lời giải chi tiết cho từng câu hỏi. Dưới đây là lời giải mẫu:
Giả sử câu hỏi là: “Một người đi xe đạp với vận tốc 15km/h. Hãy viết hàm số biểu diễn quãng đường đi được của người đó theo thời gian.”
Lời giải:
Gọi s là quãng đường đi được (km) và t là thời gian đi (giờ). Ta có hàm số:
s = 15t
Hàm số này biểu diễn mối quan hệ giữa quãng đường đi được và thời gian đi của người đó.
Giả sử câu hỏi là: “Vẽ đồ thị của hàm số y = 2x + 1.”
Lời giải:
Để vẽ đồ thị của hàm số y = 2x + 1, ta cần xác định hai điểm thuộc đồ thị. Ví dụ, ta có thể chọn:
Nối hai điểm A và B, ta được đồ thị của hàm số y = 2x + 1.
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Ngoài Sách bài tập Toán 9 - Cánh Diều tập 2, bạn có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ giải bài 39 trang 39 Sách bài tập Toán 9 - Cánh Diều tập 2 một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!