Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 9 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
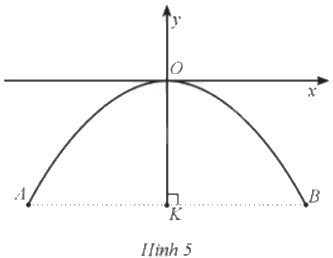
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol (y = - frac{1}{8}{x^2}), với gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Đề bài
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol \(y = - \frac{1}{8}{x^2}\), với gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Phương pháp giải - Xem chi tiết
Bước 1: Tìm tọa độ của K, từ đó tìm được tung độ của B.
Bước 2: Thay tọa độ B vào hàm số \(y = - \frac{1}{8}{x^2}\) (hoành độ của B là ẩn), từ đó tìm được hoành độ của B.
Bước 3: Tìm KB, AB.
Lời giải chi tiết
Vì \(OK = 4,5\)m và K nằm phía dưới trục Ox nên \(K\left( {0; - 4,5} \right)\).
Gọi hoành độ của B là b, tung độ của B bằng tung độ của K nên \(B\left( {b; - 4,5} \right)\).
Mặt khác, B thuộc đồ thị hàm số \(y = - \frac{1}{8}{x^2}\) nên ta có: \( - 4,5 = - \frac{1}{8}.{b^2}\)do đó \(b = 6\)
hay \(KB = 6m\).
Ta có \(AB = 2KB = 2.6 = 12\)m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất là 12m.
Bài 9 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như các tính chất của hàm số.
Bài 9 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập.
Để xác định hệ số góc và tung độ gốc của hàm số, ta cần đưa hàm số về dạng y = ax + b. Trong đó, a là hệ số góc và b là tung độ gốc.
Ví dụ: Cho hàm số y = 2x - 3. Ta có a = 2 và b = -3.
Để vẽ đồ thị của hàm số, ta cần xác định ít nhất hai điểm thuộc đồ thị. Sau đó, ta nối hai điểm này lại với nhau bằng một đường thẳng.
Ví dụ: Với hàm số y = 2x - 3, ta có thể chọn hai điểm A(0; -3) và B(1; -1). Nối hai điểm này lại với nhau, ta được đồ thị của hàm số.
Để tìm tọa độ giao điểm của đồ thị với trục Ox, ta cho y = 0 và giải phương trình để tìm x. Tọa độ giao điểm là (x; 0).
Để tìm tọa độ giao điểm của đồ thị với trục Oy, ta cho x = 0 và giải phương trình để tìm y. Tọa độ giao điểm là (0; y).
Các bài toán ứng dụng của hàm số thường yêu cầu học sinh sử dụng kiến thức về hàm số để giải quyết các vấn đề thực tế. Ví dụ, bài toán về việc tính quãng đường đi được của một vật chuyển động đều.
Ngoài bài 9 trang 58, học sinh có thể gặp các dạng bài tập tương tự như sau:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, học sinh nên:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh đã có thể tự tin giải bài 9 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hệ số góc | Số a trong hàm số y = ax + b. |
| Tung độ gốc | Số b trong hàm số y = ax + b. |