Bài 17 trang 85 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 17 trang 85 Sách bài tập Toán 9 - Cánh Diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
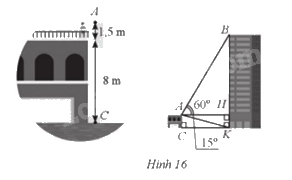
Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là \(\widehat {BAH} = 60^\circ \). Bạn Đức cũng nhìn thấy vị trí K tại chân tòa nhà đó với góc tạo bởi tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK tại H (Hình 16). Tính chiều cao BK của tòa nhà (làm tròn kết quả đến hàng phần mười của mét).
Đề bài
Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là \(\widehat {BAH} = 60^\circ \). Bạn Đức cũng nhìn thấy vị trí K tại chân tòa nhà đó với góc tạo bởi tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK tại H (Hình 16). Tính chiều cao BK của tòa nhà (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Tính HK.
Bước 2: Tính AH dựa vào hệ thức lượng trong tam giác vuông AHK.
Bước 3: Tính BH dựa vào hệ thức lượng trong tam giác vuông AHB.
Bước 4: Chiều cao của tòa nhà là BK = HK + BH.
Lời giải chi tiết
Xét CAHK có \(\widehat {ACK} = \widehat {CKH} = \widehat {KHA} = 90^\circ \) nên CAHK là hình chữ nhật.
Suy ra \(HK = CA = 8 + 1,5 = 9,5\)m.
Xét tam giác vuông AHK có \(\tan \widehat {HAK} = \frac{{HK}}{{AH}}\) do đó \(AH = \frac{{HK}}{{\tan \widehat {HAK}}} = \frac{{9,5}}{{\tan 15^\circ }}\).
Xét tam giác vuông AHB có \(\tan \widehat {HAB} = \frac{{HB}}{{AH}}\) do đó \(BH = \tan \widehat {HAB}.AH = \tan 60^\circ .\frac{{9,5}}{{\tan 15^\circ }}.\)
Chiều cao của tòa nhà là:
\(BK = HK + BH = 9,5 + \tan 60^\circ .\frac{{9,5}}{{\tan 15^\circ }} \approx 70,9m.\)
Bài 17 trong sách bài tập Toán 9 - Cánh Diều tập 1 tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán liên quan đến thực tế. Nội dung bài tập thường xoay quanh việc xác định hàm số, tìm điểm thuộc đồ thị hàm số, và giải các bài toán có tính ứng dụng cao.
Bài 17 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 17 trang 85, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày cách tiếp cận chung và các bước giải quyết vấn đề.)
Bài tập: Một người đi xe máy với vận tốc 40km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian.
Lời giải:
Để giải tốt các bài tập về hàm số, các em học sinh cần:
Hàm số là một khái niệm cơ bản và quan trọng trong Toán học. Việc nắm vững kiến thức về hàm số sẽ giúp các em học sinh:
Bài 17 trang 85 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập hữu ích giúp các em học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học Toán 9.