Bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình thoi ABCD có cạnh AB = 5cm, đường chéo AC = 8cm. Vẽ các đường tròn (A; 5cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).
Đề bài
Cho hình thoi ABCD có cạnh AB = 5cm, đường chéo AC = 8cm. Vẽ các đường tròn (A; 5cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn độ dài 2 cung theo công thức \(l = \frac{{\pi Rn}}{{180}}\).
Bước 2: Lập tỉ số 2 độ dài cung vừa tìm được.
Lời giải chi tiết
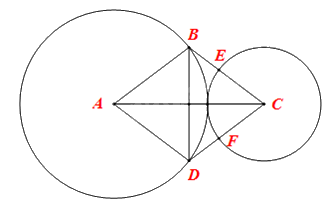
Do ABCD là hình thoi nên \(\widehat {BAD} = \widehat {BCD} = n^\circ \).
Độ dài cung nhỏ BD của (A;5cm) là:
\({l_1} = \frac{{\pi {R_1}n}}{{180}} = \frac{{\pi .5.n}}{{180}} = \frac{{\pi n}}{{36}}\).
Độ dài cung nhỏ EF của (C;3cm) là:
\({l_2} = \frac{{\pi {R_2}n}}{{180}} = \frac{{\pi .3.n}}{{180}} = \frac{{\pi n}}{{60}}\).
Tỉ số độ dài cung nhỏ BD cỉa (A) và cung nhỏ EF của (C) là:
\(\frac{{{l_1}}}{{{l_2}}} = \frac{{\pi n}}{{36}}:\frac{{\pi n}}{{60}} = \frac{5}{3}\).
Bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là đề bài chi tiết:
(Đề bài bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1 được chèn vào đây)
Để giải bài 39, ta thực hiện các bước sau:
(Lời giải chi tiết bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1 được trình bày chi tiết, bao gồm các bước giải, giải thích rõ ràng từng bước và kết quả cuối cùng)
Để giúp các em hiểu rõ hơn về cách giải bài 39, chúng ta cùng xem xét một ví dụ minh họa:
(Ví dụ minh họa bài toán tương tự bài 39, có lời giải chi tiết)
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em có thể luyện tập thêm với các bài tập sau:
Bài 39 trang 121 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp các em học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến hàm số bậc nhất. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em sẽ nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Giao điểm với trục tung |