Bài 10.12 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về các định lý đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 10.12 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
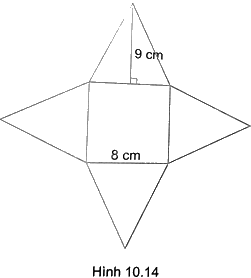
Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.
Đề bài
Sau khi cắt và gấp miếng bìa như Hình 10.14, ta được một hình chóp tứ giác đều. Tính diện tích toàn phần của tứ giác đều tạo thành.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích toàn phần của hình chóp tứ giác đều để tính diện tích toàn phần hình chóp: Diện tích toàn phần của hình chóp tứ giác đều bằng tổng diện tích xung quanh và diện tích của mặt đáy.
Lời giải chi tiết
Diện tích xung quanh của hình chóp tứ giác đều là: ${{S}_{xq}}=\frac{1}{2}4.8.9=144\left( c{{m}^{2}} \right)$
Diện tích mặt đáy là: ${{S}_{đ}}={{8}^{2}}=64\left( c{{m}^{2}} \right)$
Diện tích toàn phần của hình chóp tứ giác đều là: ${{S}_{tp}}={{S}_{đ}}+{{S}_{xq}}=144+64=208\left( c{{m}^{2}} \right)$
Bài 10.12 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức yêu cầu học sinh giải quyết một bài toán liên quan đến hình học, cụ thể là việc chứng minh các tính chất của hình thang cân. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích các yếu tố này để tìm ra mối liên hệ và hướng giải quyết phù hợp.
Thông thường, để chứng minh một hình thang là hình thang cân, ta có thể sử dụng một trong các cách sau:
(Giả sử đề bài là: Cho hình thang ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng: a) EA = EB; b) Nếu AB = CD thì ABCD là hình thang cân.)
Xét tam giác ADE và tam giác BCE:
Do đó, tam giác ADE đồng dạng với tam giác BCE (g-g). Suy ra: EA/EB = AD/BC. Tuy nhiên, để chứng minh EA = EB, cần có thêm điều kiện AD = BC, tức là hình thang ABCD là hình thang cân.
Nếu AB = CD, thì hình thang ABCD là hình thang cân. Điều này có nghĩa là AD = BC. Từ đó, theo chứng minh ở phần a, ta có EA = EB.
Ngoài ra, ta có thể chứng minh hình thang ABCD là hình thang cân bằng cách chứng minh hai góc kề một cạnh bên bằng nhau, ví dụ ∠A = ∠B.
Để nắm vững kiến thức về hình thang cân và các tính chất liên quan, học sinh nên luyện tập thêm các bài tập tương tự. Các bài tập này có thể tìm thấy trong sách bài tập Toán 8 - Kết Nối Tri Thức hoặc trên các trang web học toán online.
Bài 10.12 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân và các tính chất liên quan. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.