Bài 9.26 trang 56 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của phương trình bậc nhất một ẩn. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.26 trang 56, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho tam giác ABC với \(AB = 6cm,AC = 9cm.\) Lấy điểm D trên cạnh AC sao cho \(AD = 4cm.\)
Đề bài
Cho tam giác ABC với \(AB = 6cm,AC = 9cm.\) Lấy điểm D trên cạnh AC sao cho \(AD = 4cm.\) Chứng minh rằng $\Delta ABD\backsim \Delta ACB$ và \(BC = \frac{3}{2}BD\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – góc – cạnh): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
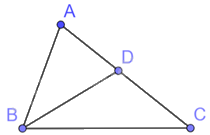
Tam giác ABD và tam giác ACB có:
\(\widehat A\;chung,\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\left( {do\;\frac{6}{9} = \frac{4}{6}} \right)\)
Do đó, $\Delta ABD\backsim \Delta ACB\left( c-g-c \right)$
Suy ra: \(\frac{{BD}}{{BC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\) nên \(BC = \frac{3}{2}BD\)
Bài 9.26 trang 56 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải một bài toán thực tế liên quan đến việc tính toán chi phí và lợi nhuận. Bài toán thường được trình bày dưới dạng một tình huống cụ thể, đòi hỏi học sinh phải đọc kỹ đề bài, xác định các yếu tố quan trọng và xây dựng phương trình bậc nhất một ẩn để giải quyết.
Bước đầu tiên để giải bài toán này là phân tích đề bài một cách cẩn thận. Xác định rõ các đại lượng đã cho và đại lượng cần tìm. Sau đó, đặt ẩn số cho đại lượng cần tìm. Ví dụ, nếu bài toán yêu cầu tính số lượng sản phẩm cần bán để đạt được lợi nhuận nhất định, ta có thể đặt ẩn số là 'x' đại diện cho số lượng sản phẩm đó.
Dựa trên các thông tin đã cho trong đề bài và ẩn số đã đặt, ta xây dựng phương trình bậc nhất một ẩn. Phương trình này thể hiện mối quan hệ giữa các đại lượng trong bài toán. Ví dụ, nếu bài toán cho biết giá thành của mỗi sản phẩm, giá bán của mỗi sản phẩm và tổng chi phí, ta có thể xây dựng phương trình để tính lợi nhuận.
Sau khi đã xây dựng được phương trình bậc nhất một ẩn, ta tiến hành giải phương trình để tìm ra giá trị của ẩn số. Có nhiều phương pháp để giải phương trình bậc nhất một ẩn, như phương pháp chuyển vế, phương pháp cộng đại số, hoặc sử dụng các công thức đã học.
Sau khi đã tìm được giá trị của ẩn số, ta cần kiểm tra lại kết quả để đảm bảo rằng nó phù hợp với điều kiện của bài toán. Nếu kết quả không hợp lý, ta cần xem xét lại các bước giải và tìm ra lỗi sai. Cuối cùng, ta trả lời bài toán bằng cách trình bày rõ ràng kết quả đã tìm được.
Giả sử bài toán có nội dung như sau: Một cửa hàng bán lẻ mua một lô hàng gồm 100 chiếc áo sơ mi với giá 80.000 đồng/chiếc. Cửa hàng bán mỗi chiếc áo sơ mi với giá 120.000 đồng. Hỏi cửa hàng thu được lợi nhuận bao nhiêu đồng?
Tổng chi phí mua hàng: 100 * 80.000 = 8.000.000 đồng
Tổng doanh thu bán hàng: 100 * 120.000 = 12.000.000 đồng
Lợi nhuận = Tổng doanh thu - Tổng chi phí
x = 12.000.000 - 8.000.000
Ngoài bài 9.26, sách bài tập Toán 8 Kết nối tri thức còn có nhiều bài tập tương tự liên quan đến ứng dụng của phương trình bậc nhất một ẩn. Các bài tập này thường yêu cầu học sinh giải quyết các vấn đề thực tế như tính toán chi phí, lợi nhuận, quãng đường, thời gian, hoặc các đại lượng vật lý khác.
Để giải các bài tập này, học sinh cần nắm vững các bước sau:
Để học tốt môn Toán 8, học sinh cần:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 9.26 trang 56 sách bài tập Toán 8 Kết nối tri thức sẽ giúp các em học sinh hiểu rõ hơn về bài toán và tự tin hơn trong các bài kiểm tra. Chúc các em học tốt!