Bài 3.12 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc trong một tam giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.12 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng;
Đề bài
Xét hai hình bình hành MNBA và MNCB.
a) Chứng minh A, B, C là ba điểm thẳng hàng;
b) Chứng minh B là trung điểm của AC;
c) Hỏi tam giác MAB thỏa mãn điều kiện gì để MNCA là một hình thang cân?
d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thỏa mãn điều kiện gì để MNDA là một hình thang cân?
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối song song.
b) Sử dụng kiến thức tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau.
c, d) Sử dụng kiến thức dấu hiệu nhận biết hình thang cân để tìm điều kiện: Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết
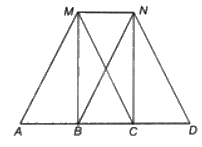
a) Vì tứ giác MNBA là hình bình hành nên MN//AB
Vì tứ giác MNCB là hình bình hành nên MN//BC
Do đó, AB và BC trùng nhau (tiên đề Euclid)
Vậy A, B, C thẳng hàng.
b) Vì tứ giác MNBA là hình bình hành nên \(MN = AB\)
Vì tứ giác MNCB là hình bình hành nên \(MN = BC\)
Do đó, \(AB = BC\)
Mà A, B, C thẳng hàng nên B là trung điểm của AC.
c) Vì MNCB là hình bình hành nên NC//MB
Do đó, \(\widehat {NCB} = \widehat {MBA}\) (hai góc đồng vị) (1)
Để MNCA là hình thang cân thì \(\widehat {NCB} = \widehat {MAB}\) (2)
Từ (1) và (2) ta có: \(\widehat {MAB} = \widehat {MBA}\)
Do đó, tam giác MAB cân tại M.
Vậy để MNCA là hình thang cân thì cần thêm điều kiện tam giác MAB cân tại M.
d) Vì MNDC là hình bình hành nên MC//ND.
Do đó, \(\widehat D = \widehat {MCA}\)
Điều kiện để MNDA là hình thang cân là \(\widehat A = \widehat D\)
Suy ra, \(\widehat {MCA} = \widehat A\). Khi đó, tam giác MCA cân tại M.
Mà MB là trung tuyến của tam giác nên MB là đường cao của tam giác, hay \(MB \bot AB\) tại B.
Vậy để MNDA là một hình thang cân thì tam giác AMB vuông tại B.
Bài 3.12 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về các tính chất của góc trong tam giác và cách vận dụng chúng vào giải quyết vấn đề. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ những thông tin đã cho và những điều cần tìm. Trong bài 3.12, đề bài thường mô tả một tình huống thực tế liên quan đến các góc trong một tam giác, và yêu cầu chúng ta tính toán các góc đó.
Để giải bài tập này, chúng ta cần nhớ lại các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài 3.12 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống (ví dụ minh họa, cần thay đổi nội dung tùy theo đề bài cụ thể):
Ví dụ: Cho tam giác ABC có góc A = 60 độ, góc B = 50 độ. Tính góc C.
Giải:
Áp dụng định lý về tổng ba góc trong một tam giác, ta có:
Góc C = 180 độ - Góc A - Góc B
Góc C = 180 độ - 60 độ - 50 độ
Góc C = 70 độ
Ngoài bài 3.12, sách bài tập Toán 8 - Kết nối tri thức với cuộc sống còn có nhiều bài tập tương tự về các góc trong tam giác. Để nắm vững kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm các bài tập sau:
Để giải bài tập về các góc trong tam giác một cách nhanh chóng và chính xác, các em có thể áp dụng một số mẹo sau:
Kiến thức về các góc trong tam giác có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, hàng hải, và đo đạc. Ví dụ, các kiến trúc sư sử dụng kiến thức này để thiết kế các công trình đảm bảo tính thẩm mỹ và độ bền vững. Các kỹ sư xây dựng sử dụng kiến thức này để tính toán các góc độ và kích thước của các bộ phận công trình.
Bài 3.12 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về các góc trong tam giác và rèn luyện kỹ năng giải bài tập. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.