Bài 10.7 trang 73 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc trong một tam giác. Bài tập này thường yêu cầu học sinh phải phân tích hình vẽ, xác định các góc đã biết và sử dụng các tính chất của tam giác để tính toán các góc còn lại.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.7 trang 73, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8).
Đề bài
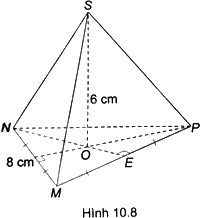
Cho hình chóp tam giác đều S.MNP có cạnh đáy bằng 8cm, đường cao bằng 6cm (H.10.8). Hãy tính thể tích của hình chóp S.MNP. Cho biết $\sqrt{48}\approx 6,9$
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích của hình chóp tam giác đều để tính thể tích hình chóp tam giác đều S. MNP: Thể tích của hình chóp tam giác đều bằng $\frac{1}{3}$ tích của diện tích đáy với chiều cao của nó.
Lời giải chi tiết
Gọi NE là đường trung tuyến của tam giác MNP và O là giao điểm của hai đường trung tuyến trong tam giác MNP. Do đó SO là chiều cao của hình chóp nên $SO=6cm$
Tam giác MNP là tam giác đều nên NE là đường trung tuyến đồng thời là đường cao. Do đó, $ME=EP=\frac{1}{2}MP=4\left( cm \right)$
Tam giác MEN vuông tại E nên $M{{E}^{2}}+N{{E}^{2}}=M{{N}^{2}}$ (định lí Pythagore)
$N{{E}^{2}}=64-16=48$ nên $NE=\sqrt{48}\approx 6,9\left( cm \right)$
Thể tích của hình chóp S.MNP là:
$V=\frac{1}{3}{{S}_{MNE}}.SO=\frac{1}{3}.\frac{1}{2}.MN.NE.SO=\frac{1}{6}.8.6,9.6=55,2\left( c{{m}^{3}} \right)$
Bài 10.7 trang 73 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về tổng ba góc trong một tam giác để giải quyết bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ những thông tin đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp hình vẽ minh họa và một số dữ kiện về các góc trong tam giác. Nhiệm vụ của học sinh là tính toán các góc còn lại dựa trên các dữ kiện đã cho.
Kiến thức cơ bản cần nhớ là tổng ba góc trong một tam giác luôn bằng 180 độ. Công thức này là nền tảng để giải quyết hầu hết các bài toán liên quan đến góc trong tam giác.
Giả sử trong một tam giác ABC, ta có góc A = 60° và góc B = 80°. Hãy tính góc C.
Áp dụng công thức, ta có: C = 180° - 60° - 80° = 40°.
Vậy, góc C của tam giác ABC là 40°.
Để củng cố kiến thức, bạn có thể tự giải thêm một số bài tập tương tự. Ví dụ:
Kiến thức về góc trong tam giác có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và thực tế, như:
Bài 10.7 trang 73 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập cơ bản nhưng quan trọng, giúp học sinh nắm vững kiến thức về tổng ba góc trong một tam giác. Bằng cách áp dụng các kiến thức đã học và luyện tập thường xuyên, các em học sinh sẽ tự tin giải quyết các bài toán tương tự và ứng dụng kiến thức vào thực tế.
Giaitoan.edu.vn hy vọng rằng hướng dẫn chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về cách giải bài 10.7 trang 73 và đạt kết quả tốt trong môn Toán 8.