Bài 3.14 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc tạo bởi đường thẳng cắt hai đường thẳng song song để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.14 trang 37, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.
Đề bài
Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.
(Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có:
+ Các cạnh đối bằng nhau và song song.
+ Các góc đối bằng nhau.
Lời giải chi tiết
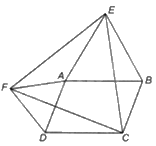
Vì ABCD là hình bình hành nên \(AB = CD,AD = BC\), \(\widehat {ADC} = \widehat {ABC} = {180^0} - \widehat {BAD}\)
Vì \(\Delta \)ABE đều nên \(AE = EB = AB\); \(\widehat {EAB} = \widehat {ABE} = \widehat {AEB} = {60^0}\)
Vì \(\Delta \)ADF đều nên \(AD = DF = AF\); \(\widehat {FAD} = \widehat {FDA} = \widehat {ADF} = {60^0}\)
Ta có: \(\widehat {FAE} = {360^0} - \widehat {EAB} - \widehat {DAB} - \widehat {FAD} = {240^0} - \widehat {DAB}\)
\(\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + {180^0} - \widehat {DAB} = {240^0} - \widehat {DAB}\)
Do đó, \(\widehat {FAE} = \widehat {FDC}\)
Tam giác AEF và tam giác DCF có:
\(AF = DF\left( {cmt} \right),\widehat {FAE} = \widehat {FDC}\left( {cmt} \right),AE = DC\left( { = AB} \right)\)
Suy ra \(\Delta AEF = \Delta DCF\left( {c - g - c} \right)\), do đó, \(FE = CF\left( 1 \right)\)
Ta có: \(\widehat {FDC} = \widehat {FDA} + \widehat {ADC} = {60^0} + \widehat {ABC} = \widehat {ABE} + \widehat {ABC} = \widehat {EBC}\)
Tam giác EBC và tam giác FDC có:
\(BC = DF\left( { = AD} \right),\widehat {EBC} = \widehat {FDC}\left( {cmt} \right),EB = DC\left( { = AB} \right)\)
Suy ra \(\Delta BEC = \Delta DCF\left( {c - g - c} \right)\), do đó, \(EC = CF\left( 2 \right)\)
Từ (1) và (2) ta có: \(EC = CF = FE\) nên tam giác FEC đều.
Bài 3.14 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh giải quyết một bài toán liên quan đến các góc tạo bởi đường thẳng cắt hai đường thẳng song song. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Giả sử đề bài là: Cho hình vẽ, biết góc A1 = 60 độ. Tính các góc còn lại.)
Lời giải:
Kết luận: Các góc còn lại lần lượt là: A2 = 120 độ, B1 = 60 độ, B2 = 120 độ, C1 = 120 độ, C2 = 60 độ.
Để nắm vững kiến thức về các góc tạo bởi đường thẳng cắt hai đường thẳng song song, các em học sinh nên luyện tập thêm các bài tập tương tự. Các bài tập này thường yêu cầu học sinh vận dụng các tính chất của các góc so le trong, đồng vị, trong cùng phía để tính các góc chưa biết.
Ví dụ:
Các em có thể tìm thấy các bài tập tương tự trong sách bài tập Toán 8 - Kết nối tri thức với cuộc sống hoặc trên các trang web học toán online.
Khi giải bài tập về góc, các em học sinh nên:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 3.14 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán!