Bài 9.8 trang 52 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình hộp chữ nhật và hình lập phương vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.8, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.
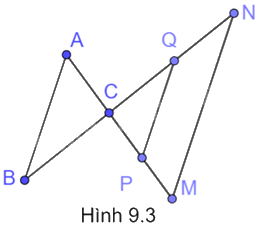
Trong Hình 9.3, cho PQ và MN cùng song song với AB. Hãy liệt kê ba cặp tam giác phân biệt đồng dạng với nhau.
Đề bài
Trong Hình 9.3, cho PQ và MN cùng song song với AB. Hãy liệt kê ba cặp tam giác phân biệt đồng dạng với nhau.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức định lí (một trường hợp đặc biệt của hai tam giác đồng dạng) để chứng minh hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
Tam giác CMN có: PQ//MN nên $\Delta CMN\backsim \Delta CPQ$
Tam giác CMN có: AB//MN nên $\Delta CMN\backsim \Delta CAB$
Tam giác CPQ có: PQ//AB nên $\Delta CPQ\backsim \Delta CAB$
Bài 9.8 yêu cầu chúng ta giải quyết một bài toán liên quan đến hình hộp chữ nhật và việc tính toán thể tích. Để hiểu rõ hơn về cách tiếp cận và giải quyết bài toán này, chúng ta sẽ cùng nhau phân tích từng bước.
Đề bài thường mô tả một hình hộp chữ nhật với các kích thước cụ thể hoặc đưa ra mối quan hệ giữa các kích thước. Yêu cầu của bài toán có thể là tính thể tích, diện tích bề mặt, hoặc tìm một kích thước khi biết các kích thước khác.
Giả sử đề bài cho: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính thể tích của hình hộp chữ nhật đó.
Lời giải:
Áp dụng công thức tính thể tích hình hộp chữ nhật, ta có:
V = 5cm * 3cm * 4cm = 60cm3
Vậy thể tích của hình hộp chữ nhật là 60cm3.
Việc nắm vững các công thức và phương pháp giải bài tập về hình hộp chữ nhật là rất quan trọng trong chương trình Toán 8. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải quyết các bài toán liên quan đến chủ đề này. Chúc các em học tập tốt!