Bài 5.14 trang 67 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.14 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bình vẽ biểu đồ sau đây để biểu diễn tỉ lệ học sinh trong lớp tham gia vào các câu lạc bộ (CLB) tiếng Anh, tiếng Pháp, tiếng Trung của trường.
Đề bài
Bình vẽ biểu đồ sau đây để biểu diễn tỉ lệ học sinh trong lớp tham gia vào các câu lạc bộ (CLB) tiếng Anh, tiếng Pháp, tiếng Trung của trường.
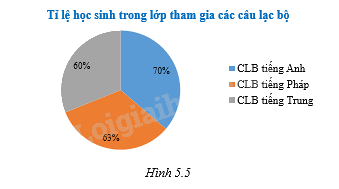
Hãy cho biết biểu đồ này có điểm nào không hợp lí.
Phương pháp giải - Xem chi tiết
Hãy cho biết biểu đồ này có điểm nào không hợp lí.
Lời giải chi tiết
Trong biểu đồ hình quạt tròn, cả hình tròn biểu diễn \(100\% \) nhưng trong biểu đồ hình tròn ở Hình 5.5 biểu diễn \(60\% + 70\% + 63\% = 193\% \) là không hợp lý.
Bài 5.14 trang 67 sách bài tập Toán 8 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về các dấu hiệu nhận biết hai đường thẳng song song để chứng minh một đường thẳng song song với một đường thẳng khác. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Giả sử đề bài cụ thể của bài 5.14 được đưa ra ở đây. Ví dụ: Cho hình vẽ, biết góc A = 60 độ, góc B = 120 độ. Chứng minh AB song song CD.)
Lời giải:
Xét hình vẽ, ta có:
Ta thấy góc A và góc B là cặp góc trong cùng phía. Mà góc A + góc B = 60 độ + 120 độ = 180 độ. Do đó, AB song song CD (theo dấu hiệu nhận biết hai đường thẳng song song).
Ngoài bài 5.14, sách bài tập Toán 8 - Kết nối tri thức còn nhiều bài tập tương tự yêu cầu học sinh vận dụng các dấu hiệu nhận biết hai đường thẳng song song. Để giải các bài tập này, các em có thể áp dụng các phương pháp sau:
Để củng cố kiến thức về các dấu hiệu nhận biết hai đường thẳng song song, các em có thể tự giải các bài tập sau:
Bài 5.14 trang 67 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các dấu hiệu nhận biết hai đường thẳng song song. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.