Chào mừng các em học sinh đến với bài giải bài 9.45 trang 63 sách bài tập Toán 8 - Kết nối tri thức. Bài viết này sẽ cung cấp cho các em lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những bài giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng từng bước để các em có thể tự học và ôn tập hiệu quả.
Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:
a) $\Delta ABC\backsim \Delta HAC$ và \(C{A^2} = CH.CB\)
b) \(\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để chứng minh hai tam giác đồng dạng: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết
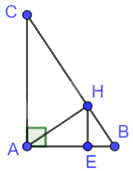
Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\).
Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C\) chung
Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$
Suy ra: \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên \(C{A^2} = CH.CB\)
b) Vì HE vuông góc với AB (E thuộc AB) nên \(\widehat {AEH} = {90^0}\)
Tam giác AHE và tam giác CBA có:
\(\widehat {AEH} = \widehat {BAC} = {90^0},\widehat {HAE} = \widehat C\) (cùng phụ với góc CAH)
Do đó, $\Delta AHE\backsim \Delta CBA\left( g-g \right)$. Suy ra \(\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}\)
Bài 9.45 trang 63 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về các dạng toán liên quan đến hình học, đặc biệt là các tính chất của hình thang cân. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin đã cho. Thông thường, đề bài sẽ cung cấp các dữ kiện về độ dài các cạnh, góc hoặc đường chéo của hình thang cân. Dựa vào các dữ kiện này, chúng ta sẽ sử dụng các tính chất và công thức đã học để tìm ra kết quả cần tìm.
(Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.)
Lời giải:
Vậy chiều cao của hình thang ABCD là khoảng 5.45cm.
Ngoài bài 9.45, còn rất nhiều bài tập tương tự về hình thang cân. Các bài tập này thường yêu cầu chúng ta tính độ dài các cạnh, góc, đường chéo, diện tích hoặc chứng minh các tính chất liên quan đến hình thang cân. Để giải các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức và kỹ năng giải bài tập về hình thang cân, các em nên luyện tập thêm với các bài tập khác trong sách bài tập và các đề thi thử. Ngoài ra, các em có thể tham khảo các tài liệu học tập trực tuyến hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè.
Bài 9.45 trang 63 sách bài tập Toán 8 - Kết nối tri thức là một bài tập điển hình về hình thang cân. Hy vọng rằng, với hướng dẫn chi tiết và các phương pháp giải đã trình bày, các em có thể tự tin giải bài tập này và các bài tập tương tự một cách hiệu quả. Chúc các em học tập tốt!