Bài 4.9 trang 50 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.9 trang 50, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng (EI = DK)
Đề bài
Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng \(EI = DK\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
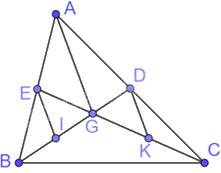
Vì BD, CE là các đường trung tuyến của tam giác ABC nên D, E lần lượt là trung điểm của AC, AB.
Tam giác ABG có I, E lần lượt là trung điểm của GB, AB nên IE là đường trung bình của tam giác ABG. Do đó, \(EI = \frac{1}{2}AG\) (1)
Tam giác AGC có D, K lần lượt là trung điểm của AC, GC nên DK là đường trung bình của tam giác AGC. Do đó, \(DK = \frac{1}{2}AG\) (2)
Từ (1) và (2) ta có: \(EI = DK\)
Bài 4.9 trang 50 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh chứng minh một tính chất liên quan đến hình thang cân. Để giải bài này, chúng ta cần nắm vững các kiến thức về:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.
Lời giải:
Kết luận: Vậy EA = EB.
Cách giải bài này dựa trên việc chứng minh hai tam giác EAB và EDC đồng dạng. Việc chứng minh hai tam giác đồng dạng là một kỹ năng quan trọng trong hình học, giúp chúng ta thiết lập các tỉ lệ thức và giải quyết các bài toán liên quan đến độ dài đoạn thẳng và góc.
Để chứng minh hai tam giác đồng dạng, chúng ta cần chứng minh ít nhất hai góc tương ứng bằng nhau. Trong bài này, chúng ta đã chứng minh được hai góc tương ứng bằng nhau (∠EAB = ∠EDC và ∠EBA = ∠ECD) nhờ vào tính chất của hình thang cân và các góc so le trong.
Sau khi chứng minh hai tam giác đồng dạng, chúng ta đã sử dụng tỉ lệ thức để thiết lập mối quan hệ giữa các đoạn thẳng. Việc sử dụng tỉ lệ thức là một công cụ mạnh mẽ trong hình học, giúp chúng ta giải quyết các bài toán liên quan đến độ dài đoạn thẳng và diện tích hình.
Ngoài bài 4.9, sách bài tập Toán 8 Kết nối tri thức còn rất nhiều bài tập thú vị và bổ ích khác. Các em học sinh nên dành thời gian làm đầy đủ các bài tập để nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Để học toán hiệu quả hơn, các em có thể tham khảo thêm các tài liệu học tập khác như sách giáo khoa, các trang web học toán online, hoặc các video bài giảng trên YouTube.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
Giả sử AB = 5cm, CD = 10cm, AD = BC = 8cm. Khi đó, ta có thể tính được EA và EB như sau:
EA/ED = AB/CD = 5/10 = 1/2
ED = EA + AD = EA + 8
EA/(EA + 8) = 1/2
2EA = EA + 8
EA = 8cm
Vậy EA = EB = 8cm.
Khi giải bài tập hình học, các em cần chú ý: