Bài 9.51 trang 64 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để tìm ra các đại lượng chưa biết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.51 trang 64, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:
a) \(AM.AB = A{H^2}\) và \(AM.AB = AN.AC\)
b) $\Delta AMN\backsim \Delta ACB$
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
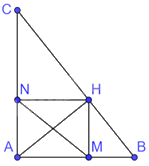
Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Vì \(AH \bot BC\) (do AH là đường cao của tam giác ABC) nên \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Vì \(HM \bot AB\) nên \(\widehat {HMA} = \widehat {HMB} = {90^0}\)
Vì \(HN \bot AC\) nên \(\widehat {HNA} = \widehat {HNC} = {90^0}\)
Tam giác AMH và tam giác AHB có:
\(\widehat {AMH} = \widehat {AHB} = {90^0},\widehat {HAB}\;chung\)
Do đó, $\Delta AMH\backsim \Delta AHB\left( g-g \right)$
Suy ra: \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\) nên \(AM.AB = A{H^2}\) (1)
Tam giác ANH và tam giác AHC có:
\(\widehat {ANH} = \widehat {AHC} = {90^0},\widehat {HAC}\;chung\)
Do đó, $\Delta ANH\backsim \Delta AHC\left( g-g \right)$
Suy ra: \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) nên \(AN.AC = A{H^2}\) (2)
Từ (1) và (2) ta có: \(AM.AB = AN.AC\)
b) Theo phần a ta có: \(AM.AB = AN.AC\) nên \(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\)
Tam giác AMN và tam giác ACB có: \(\widehat {BAC}\;chung,\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\)
Do đó, $\Delta AMN\backsim \Delta ACB\left( c-g-c \right)$
Bài 9.51 trang 64 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một ngọn cây dựa vào bóng của cây và bóng của một người. Để giải bài toán này, chúng ta cần hiểu rõ về ứng dụng của tam giác đồng dạng trong việc giải quyết các bài toán thực tế.
Một ngọn cây cao 5m, người ta đo được bóng của cây trên mặt đất là 8m. Hỏi một người cao 1,6m có bóng trên mặt đất dài bao nhiêu mét?
Bài toán này có thể được giải quyết bằng cách sử dụng tính chất của tam giác đồng dạng. Ta có thể hình dung bóng của cây và bóng của người tạo thành hai tam giác vuông đồng dạng. Tỉ lệ giữa chiều cao và bóng của cây sẽ bằng tỉ lệ giữa chiều cao và bóng của người.
Gọi chiều dài bóng của người là x (m). Ta có tỉ lệ thức sau:
5/8 = 1.6/x
Giải phương trình trên, ta được:
x = (1.6 * 8) / 5 = 2.56
Vậy, bóng của người cao 1,6m trên mặt đất dài 2,56 mét.
Bước 1: Xác định các đại lượng đã biết và đại lượng cần tìm. Trong bài toán này, ta biết chiều cao của cây (5m), chiều dài bóng của cây (8m) và chiều cao của người (1,6m). Ta cần tìm chiều dài bóng của người.
Bước 2: Phân tích mối quan hệ giữa các đại lượng. Ta nhận thấy rằng bóng của cây và bóng của người tạo thành hai tam giác vuông đồng dạng. Điều này có nghĩa là tỉ lệ giữa chiều cao và bóng của cây sẽ bằng tỉ lệ giữa chiều cao và bóng của người.
Bước 3: Lập tỉ lệ thức và giải phương trình. Dựa vào mối quan hệ giữa các đại lượng, ta lập tỉ lệ thức và giải phương trình để tìm ra giá trị của đại lượng cần tìm.
Các bài tập tương tự bài 9.51 thường yêu cầu học sinh vận dụng kiến thức về tam giác đồng dạng để giải quyết các bài toán thực tế khác, chẳng hạn như:
Để giải các bài tập về tam giác đồng dạng một cách hiệu quả, bạn nên:
Bài 9.51 trang 64 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
| Đại lượng | Giá trị |
|---|---|
| Chiều cao cây | 5m |
| Bóng cây | 8m |
| Chiều cao người | 1.6m |
| Bóng người | 2.56m |
| Bảng tổng hợp các đại lượng trong bài toán | |