Bài 2.24 trang 30 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh áp dụng các quy tắc, công thức đã học để đơn giản hóa biểu thức hoặc giải phương trình.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.24 trang 30, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Từ một miếng bìa có dạng hình tròn (H.2.4) với bán kính R (cm),
Đề bài
Từ một miếng bìa có dạng hình tròn (H.2.4) với bán kính R (cm), người ta khoét một hình tròn ở giữa có bán kính r (cm), \(r < R\).
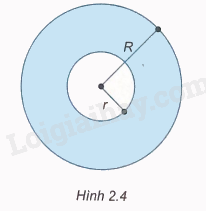
a) Viết công thức tính diện tích phần còn lại của miếng bìa.
b) Tính diện tích phần còn lại của miếng bìa biết tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm.
Phương pháp giải - Xem chi tiết
a) Ta áp dụng công thức tính diện tích hình tròn là \(\;\pi {R^2}\;\)với R là bán kính.
Diện tích phân còn lại bằng diện tích có bán kính R trừ đi diện tích miếng bìa hình tròn có bán kính r.
b) Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)rồi thay tổng và hiệu của hai bán kính vào biểu thức.
Lời giải chi tiết
a) Diện tích miếng bìa hình tròn có bán kính R (cm) là: \(\;\pi {R^2}\;\left( {c{m^2}} \right)\).
Diện tích miếng bìa hình tròn có bán kính r (cm) là: \(\pi {r^2}\;(c{m^2})\).
Diện tích phần còn lại của miếng bìa là:\(\pi {R^2}\; - \pi {r^2}\; = \pi ({R^2}\;-{r^2})(c{m^2}).\)
b) Ta có: \(\pi {R^2}\; - \pi {r^2}\; = \pi ({R^2}\;-{r^2}){\rm{ = }}\;\pi \left( {R-r} \right)\left( {R + r} \right)(*).\)
Do tổng hai bán kính là 10 cm và hiệu hai bán kính là 3 cm nên ta có:
\(R + r = 10\) và \(R - r = 3\).
Thay vào \((*)\) ta được: \(\pi \left( {10 - 3} \right)\left( {10 + 3} \right) = \pi .7.13 = 91\pi .\)
Vậy diện tích phần còn lại của miếng bìa là \(91\pi \left( {c{m^2}} \right).\)
Bài 2.24 trang 30 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh thực hiện các phép biến đổi đại số để tìm giá trị của biểu thức hoặc giải phương trình. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu ngoặc, thứ tự thực hiện các phép toán, và các công thức biến đổi đại số.
Trước khi bắt đầu giải bài, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Đề bài có thể yêu cầu bạn:
Lời giải:
2x + 3(x - 1) = 2x + 3x - 3 = 5x - 3
Các kiến thức và kỹ năng được học trong bài 2.24 trang 30 có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học. Việc nắm vững các quy tắc biến đổi đại số sẽ giúp bạn giải quyết các bài toán phức tạp hơn một cách dễ dàng và hiệu quả.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 2.24 trang 30 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán đại số. Bằng cách nắm vững các quy tắc và thực hành thường xuyên, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.
| Khái niệm | Giải thích |
|---|---|
| Biểu thức đại số | Một dãy các số, chữ và các phép toán. |
| Phương trình | Một đẳng thức chứa ẩn số. |
| Rút gọn biểu thức | Biến đổi biểu thức thành dạng đơn giản hơn. |
| Nguồn: Giaitoan.edu.vn | |