Bài 4.16 trang 55 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các yếu tố hình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc trong tam giác, tính chất đường trung tuyến và đường cao để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.16 trang 55, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD.
Đề bài
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh \(MI = IK = KN\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
+ Sử dụng kiến thức về định lí Thalès đảo để chứng minh: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
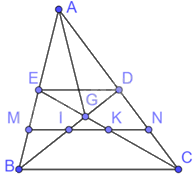
Vì CE là trung tuyến của tam giác ABC nên \(AE = EB\)
Vì M là trung điểm của BE nên \(EM = \frac{1}{2}EB\)
Do đó, \(\frac{{EM}}{{AE}} = \frac{1}{2}\) (1)
Vì BD là trung tuyến của tam giác ABC nên \(AD = DC\)
Vì N là trung điểm của DC nên \(DN = \frac{1}{2}CD\)
Do đó, \(\frac{{DN}}{{AD}} = \frac{1}{2}\) (2)
Từ (1) và (2) ta có: \(\frac{{EM}}{{AE}} = \frac{{DN}}{{AD}}\)
Tam giác AMN có: \(\frac{{EM}}{{AE}} = \frac{{DN}}{{AD}}\) nên ED//MN
Tam giác EBD có: MI//ED (cmt), M là trung điểm của BE nên I là trung điểm BD. Do đó, \(\frac{{MI}}{{ED}} = \frac{1}{2}\) (1)
Tam giác ECD có: NK//ED (cmt), N là trung điểm của DC nên K là trung điểm EC. Do đó, \(\frac{{KN}}{{ED}} = \frac{1}{2}\) (2)
Tam giác ABC có E, D lần lượt là trung điểm của AB, AC nên ED là đường trung bình của tam giác ABC. Do đó, \(\frac{{ED}}{{BC}} = \frac{1}{2}\) (3) và ED//BC
Từ (1), (2), (3) có: \(\frac{{MI}}{{BC}} = \frac{{KN}}{{BC}} = \frac{1}{4}\) (4)
Tam giác EBC có: KM//BC (cùng song song với ED), M là trung điểm của BE nên K là trung điểm của EC.
Do đó, MK là đường trung bình của tam giác EBC.
Suy ra: \(\frac{{MK}}{{BC}} = \frac{1}{2}\), hay \(\frac{{MI + IK}}{{BC}} = \frac{1}{2}\), mà \(\frac{{MI}}{{BC}} = \frac{1}{4}\) nên \(\frac{{IK}}{{BC}} = \frac{1}{4}\) (5)
Từ (4) và (5) ta có: \(MI = IK = KN\)
Bài 4.16 trang 55 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán các yếu tố hình học trong một tình huống cụ thể. Để giải bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về tam giác, góc, đường trung tuyến và đường cao.
Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định các thông tin đã cho và các thông tin cần tìm. Trong bài 4.16, đề bài thường cung cấp một hình vẽ hoặc một mô tả về một tình huống hình học, và yêu cầu học sinh tính toán một số yếu tố như độ dài cạnh, số đo góc, hoặc diện tích.
Sau khi đã hiểu rõ yêu cầu của bài toán, học sinh cần áp dụng các kiến thức đã học để giải quyết bài toán. Các kiến thức thường được sử dụng trong bài 4.16 bao gồm:
Để minh họa cách giải bài 4.16, chúng ta hãy xem xét một ví dụ cụ thể. Giả sử đề bài yêu cầu tính độ dài cạnh BC của tam giác ABC, biết rằng góc A = 60 độ, AB = 5cm, và AC = 8cm. Để giải bài toán này, chúng ta có thể sử dụng định lý cosin:
BC2 = AB2 + AC2 - 2 * AB * AC * cosA
Thay các giá trị đã biết vào công thức, ta có:
BC2 = 52 + 82 - 2 * 5 * 8 * cos60o
BC2 = 25 + 64 - 80 * 0.5
BC2 = 49
BC = 7cm
Khi giải bài tập 4.16, học sinh cần lưu ý một số điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể luyện tập thêm các bài tập tương tự. Dưới đây là một số bài tập gợi ý:
Bài 4.16 trang 55 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế. Bằng cách nắm vững các kiến thức cơ bản và áp dụng đúng các phương pháp giải, học sinh có thể tự tin giải quyết bài toán này một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng hướng dẫn chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và đạt kết quả tốt trong học tập.