Bài 9.22 trang 56 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này thường yêu cầu học sinh chứng minh các tính chất hoặc tính toán các yếu tố liên quan đến hình thang cân.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.22 trang 56, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho \(\widehat {APQ} = \widehat {ACB}\). Chứng minh rằng:
Đề bài
Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho \(\widehat {APQ} = \widehat {ACB}\). Chứng minh rằng:
a) \(AP.AB = AQ.AC\)
b) $\Delta APC\backsim \Delta AQB$
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc): Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – góc – cạnh): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
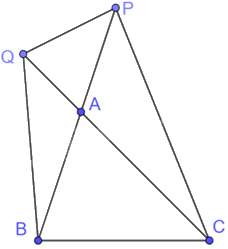
a) Tam giác APQ và tam giác ACB có:
\(\widehat {PAQ} = \widehat {BAC}\) (hai góc đối đỉnh), \(\widehat {APQ} = \widehat {ACB}\) (gt)
Do đó, $\Delta APQ\backsim \Delta ACB\left( g-g \right)$ nên \(\frac{{AP}}{{AC}} = \frac{{AQ}}{{AB}}\)
Suy ra: \(AP.AB = AQ.AC\)
b) Vì \(\frac{{AP}}{{AC}} = \frac{{AQ}}{{AB}}\) nên \(\frac{{AP}}{{AQ}} = \frac{{AC}}{{AB}}\)
Tam giác APC và tam giác AQB có:
\(\widehat {PAC} = \widehat {BAQ}\) (hai góc đối đỉnh), \(\frac{{AP}}{{AQ}} = \frac{{AC}}{{AB}}\) (cmt)
Do đó, $\Delta APC\backsim \Delta AQB\left( c-g-c \right)$
Bài 9.22 trang 56 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh chứng minh một tính chất quan trọng của hình thang cân. Để giải bài này, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng EA = EB.
Lời giải:
Giải thích chi tiết:
Bước đầu tiên, chúng ta cần xác định mối quan hệ giữa các góc và cạnh trong hình thang cân. Vì AB song song với CD, nên các góc so le trong bằng nhau. Điều này giúp chúng ta thiết lập được sự bằng nhau của các góc trong hai tam giác AED và BEC.
Tiếp theo, chúng ta sử dụng tính chất của hình thang cân để khẳng định AD = BC. Đây là một yếu tố quan trọng để áp dụng trường hợp góc - cạnh - góc.
Khi đã chứng minh được tam giác AED bằng tam giác BEC, chúng ta có thể kết luận rằng EA = EB, do đó hoàn thành chứng minh bài toán.
Lưu ý:
Khi giải các bài toán về hình thang cân, việc vẽ hình chính xác và ghi chú các yếu tố đã biết là rất quan trọng. Điều này giúp chúng ta dễ dàng nhận ra các mối quan hệ giữa các góc và cạnh, từ đó tìm ra lời giải phù hợp.
Ngoài ra, việc nắm vững các định nghĩa và tính chất của hình thang cân là điều kiện cần thiết để giải quyết các bài toán liên quan. Hãy dành thời gian ôn tập lại các kiến thức này trước khi bắt đầu giải bài tập.
Bài tập tương tự:
Để củng cố kiến thức về hình thang cân, bạn có thể thử giải các bài tập tương tự sau:
Kết luận:
Bài 9.22 trang 56 sách bài tập Toán 8 Kết nối tri thức là một bài tập điển hình về việc áp dụng các tính chất của hình thang cân. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh đã hiểu rõ cách giải bài tập này và có thể tự tin giải các bài tập tương tự.
Để hiểu sâu hơn về bài toán này, bạn có thể tham khảo thêm các kiến thức sau:
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc các bạn học tập tốt!