Chào mừng các em học sinh đến với lời giải chi tiết bài 11 trang 82 sách bài tập Toán 8 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúng tôi cam kết mang đến những tài liệu học tập chất lượng, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho (frac{{MB}}{{MA}} = frac{1}{3}), N là điểm trên cạnh BC sao cho (frac{{NB}}{{NC}} = frac{1}{3}.)
Đề bài
Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho \(\frac{{MB}}{{MA}} = \frac{1}{3}\), N là điểm trên cạnh BC sao cho \(\frac{{NB}}{{NC}} = \frac{1}{3}.\)
a) Chứng minh MN//AC và \(MN = \frac{1}{4}AC\).
b) Gọi K là giao điểm của AN và CM. Chứng minh \(\frac{{KN}}{{KA}} = \frac{{KM}}{{KC}} = \frac{1}{4}\).
c) Nếu thay điều kiện \(\frac{{MB}}{{MA}} = \frac{1}{3}\) và \(\frac{{NB}}{{NC}} = \frac{1}{3}\) bằng điều kiện CM là phân giác của góc C, AN là phân giác của góc A thì tam giác ABC phải thỏa mãn điều kiện gì để MN//AC?
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức định lí Thalés đảo để chứng minh MN//AC: Nếu một đường cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
+ Sử dụng kiến thức định lí (một trường hợp đặc biệt của hai tam giác đồng dạng) để chứng minh hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
b) Sử dụng kiến thức định lí (một trường hợp đặc biệt của hai tam giác đồng dạng) để chứng minh hai tam giác đồng dạng: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
c) Sử dụng tính chất đường phân giác của tam giác để tìm điều kiện của tam giác ABC: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
Lời giải chi tiết
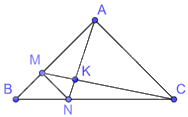
a) Xét tam giác ABC có: \(\frac{{MB}}{{MA}} = \frac{{NB}}{{NC}}\left( { = \frac{1}{3}} \right)\) nên MN//AC (định lí Thalés đảo)
Tam giác ABC có: MN//AC nên \(\Delta BMN \backsim \Delta BAC\)
Do đó,\(\frac{{MN}}{{AC}} = \frac{{BM}}{{AB}} = \frac{{BM}}{{BM + MA}} = \frac{{BM}}{{4BM}} = \frac{1}{4}\) nên \(MN = \frac{1}{4}AC\)
b) Tam giác MNK có: MN//AC nên , do đó \(\frac{{KN}}{{KA}} = \frac{{KM}}{{KC}} = \frac{{MN}}{{AC}} = \frac{1}{4}\)
c) Nếu MN//AC thì \(\frac{{MB}}{{MA}} = \frac{{NB}}{{NC}}\) (1)
Vì CM là phân giác của góc BCA trong tam giác ABC nên \(\frac{{MB}}{{MA}} = \frac{{BC}}{{AC}}\) (2)
Vì AN là phân giác của góc BAC trong tam giác ABC nên \(\frac{{NB}}{{NC}} = \frac{{AB}}{{AC}}\) (3)
Từ (1), (2) và (3) ta có: \(\frac{{AB}}{{AC}} = \frac{{BC}}{{AC}}\) nên \(AB = BC\)
Do đó, tam giác ABC cân tại B.
Ngược lại, nếu tam giác ABC cân tại B, CM là phân giác của góc C, AN là phân giác góc A thì dễ thấy MN//AC.
Vậy để MN//AC thì điều kiện là tam giác ABC cân tại B.
Bài 11 trang 82 sách bài tập Toán 8 Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hai hình này.
Bài 11 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để giải quyết bài tập này một cách hiệu quả, học sinh cần:
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật đó.
Giải:
Ví dụ 2: Một hình lập phương có cạnh 6cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương đó.
Giải:
Khi giải bài tập về hình hộp chữ nhật và hình lập phương, học sinh cần chú ý đến đơn vị đo. Đảm bảo rằng tất cả các kích thước đều được biểu diễn bằng cùng một đơn vị đo trước khi thực hiện các phép tính.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải các bài tập sau:
Bài 11 trang 82 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng, giúp học sinh hiểu sâu hơn về hình hộp chữ nhật và hình lập phương. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.
| Hình | Công thức |
|---|---|
| Hình hộp chữ nhật | Diện tích xung quanh: 2 * (d + r) * hDiện tích toàn phần: 2 * (d * r + d * h + r * h)Thể tích: d * r * h |
| Hình lập phương | Diện tích xung quanh: 6 * a2Diện tích toàn phần: 6 * a2Thể tích: a3 |