Bài 7.30 trang 30 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.30 trang 30 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hải lí (còn gọi là dặm biển) là một đơn vị chiều dài hàng hải và 1 hải lí bằng 1,852km
Đề bài
Hải lí (còn gọi là dặm biển) là một đơn vị chiều dài hàng hải và 1 hải lí bằng 1,852km
a) Viết công thức biểu thị y (km) theo x (hải lí). Giá trị âm của x có ý nghĩa gì trong tình huống này không? Giải thích.
b) Vẽ đồ thị của hàm số \(y = f\left( x \right)\) nhận được ở câu a.
c) Một hành trình đi biển dài 350 hải lí. Hỏi hành trình đó dài bao nhiêu kilômét?
Phương pháp giải - Xem chi tiết
* Sử dụng khái niệm hàm số bậc nhất để viết hàm số: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)
* Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ các đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
Lời giải chi tiết
a) Công thức biểu thị y (km) theo x (hải lí) là: \(y = 1,852x\) (km)
Giá trị âm của x trong trường hợp này không có ý nghĩa vì chiều dài là một đại lượng không âm.
b) Đồ thị hàm số \(y = 1,852x\) đi qua \(O\left( {0;0} \right)\) và \(A\left( {5;9,26} \right)\)
Đồ thị của hàm số \(y = 1,852x\) (với x không âm) là một phần đường thẳng như hình dưới.
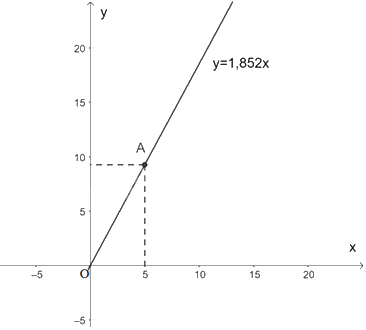
c) Với \(x = 350\) thì \(y = 1,852.350 = 648,2\left( {km} \right)\)
Bài 7.30 trang 30 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tam giác đồng dạng và các tính chất của đường thẳng song song. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết và biết cách áp dụng vào thực tế.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 7.30, học sinh cần phân tích hình vẽ, xác định các yếu tố đã cho và tìm ra mối liên hệ giữa chúng. Việc này giúp học sinh có cái nhìn tổng quan về bài toán và lựa chọn phương pháp giải phù hợp.
Tam giác đồng dạng là một khái niệm quan trọng trong hình học, được sử dụng rộng rãi trong việc giải các bài toán liên quan đến tỉ lệ và độ dài đoạn thẳng. Trong bài 7.30, học sinh có thể áp dụng các tiêu chí đồng dạng của tam giác (góc - góc, cạnh - cạnh, cạnh - góc) để chứng minh hai tam giác đồng dạng. Từ đó, suy ra các tỉ lệ tương ứng và giải quyết bài toán.
Đường thẳng song song cũng là một yếu tố quan trọng trong hình học, được sử dụng để chứng minh các góc bằng nhau, các đoạn thẳng tỉ lệ và các hình đồng dạng. Trong bài 7.30, học sinh có thể sử dụng các tính chất của đường thẳng song song để tìm ra mối liên hệ giữa các góc và đoạn thẳng trong hình vẽ.
(Phần này sẽ trình bày lời giải chi tiết của bài toán, bao gồm các bước giải, các công thức sử dụng và các giải thích rõ ràng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm bắt được phương pháp giải và tự tin làm bài tập.)
Để giúp học sinh hiểu rõ hơn về phương pháp giải bài 7.30, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự. Các ví dụ này sẽ giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán.
Khi giải bài tập hình học, học sinh cần lưu ý một số điều sau:
Bài 7.30 trang 30 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về tam giác đồng dạng và các tính chất của đường thẳng song song. Hy vọng rằng, với lời giải chi tiết và các ví dụ minh họa, học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 8 và các môn học khác.